AlwaysR, Módulo III: Estadística en R
Clase 1: Introducción. Estadística descriptiva. Distribuciones de probabilidad.
Dr. Giancarlo M. Correa

Introducción
Silabo
Revisar silabo en Cousteau Consultant Group.
También puede ser encontrado en el Google Drive.
Metodología
Preguntas: En cualquier momento. Dejar preguntas en el chat o activar micrófono.
Material: Presentaciones, códigos y videos en Google Drive. También puede ser encontrado en mi sitio web.
Metodología
Preguntas: En cualquier momento. Dejar preguntas en el chat o activar micrófono.
Material: Presentaciones, códigos y videos en Google Drive. También puede ser encontrado en mi sitio web.
Certificado: De asistencia ó aprobación (completar todos los quizzes al término de la semana).
Metodología
Preguntas: En cualquier momento. Dejar preguntas en el chat o activar micrófono.
Material: Presentaciones, códigos y videos en Google Drive. También puede ser encontrado en mi sitio web.
Certificado: De asistencia ó aprobación (completar todos los quizzes al término de la semana).
Horas de oficina: Por definir
Metodología
Preguntas: En cualquier momento. Dejar preguntas en el chat o activar micrófono.
Material: Presentaciones, códigos y videos en Google Drive. También puede ser encontrado en mi sitio web.
Certificado: De asistencia ó aprobación (completar todos los quizzes al término de la semana).
Horas de oficina: Por definir
Contacto: Escribir a cursos@cousteau-group.com ó gcorrea@uw.edu
Estadística descriptiva
Variable
Es un atributo que describe un individuo, lugar, o cosa. Este atributo puede variar entre individuos. Ejemplo: altura total, temperatura, edad, estadio sexual.
- Cuantitativa: Refleja magnitud. Representa una medida y es numérica.
Discreta: Valores que toman son contables y tienen un número finito de posibilidades.
Continua: Valores no son contables y tiene un infinito número de posibilidades.
Variable
Es un atributo que describe un individuo, lugar, o cosa. Este atributo puede variar entre individuos. Ejemplo: altura total, temperatura, edad, estadio sexual.
- Cuantitativa: Refleja magnitud. Representa una medida y es numérica.
Discreta: Valores que toman son contables y tienen un número finito de posibilidades.
Continua: Valores no son contables y tiene un infinito número de posibilidades.
- Cualitativa: No son numericas, valores son categorías.
Nominal: No existe un orden para los niveles.
Ordinal: Existe un orden para los niveles.
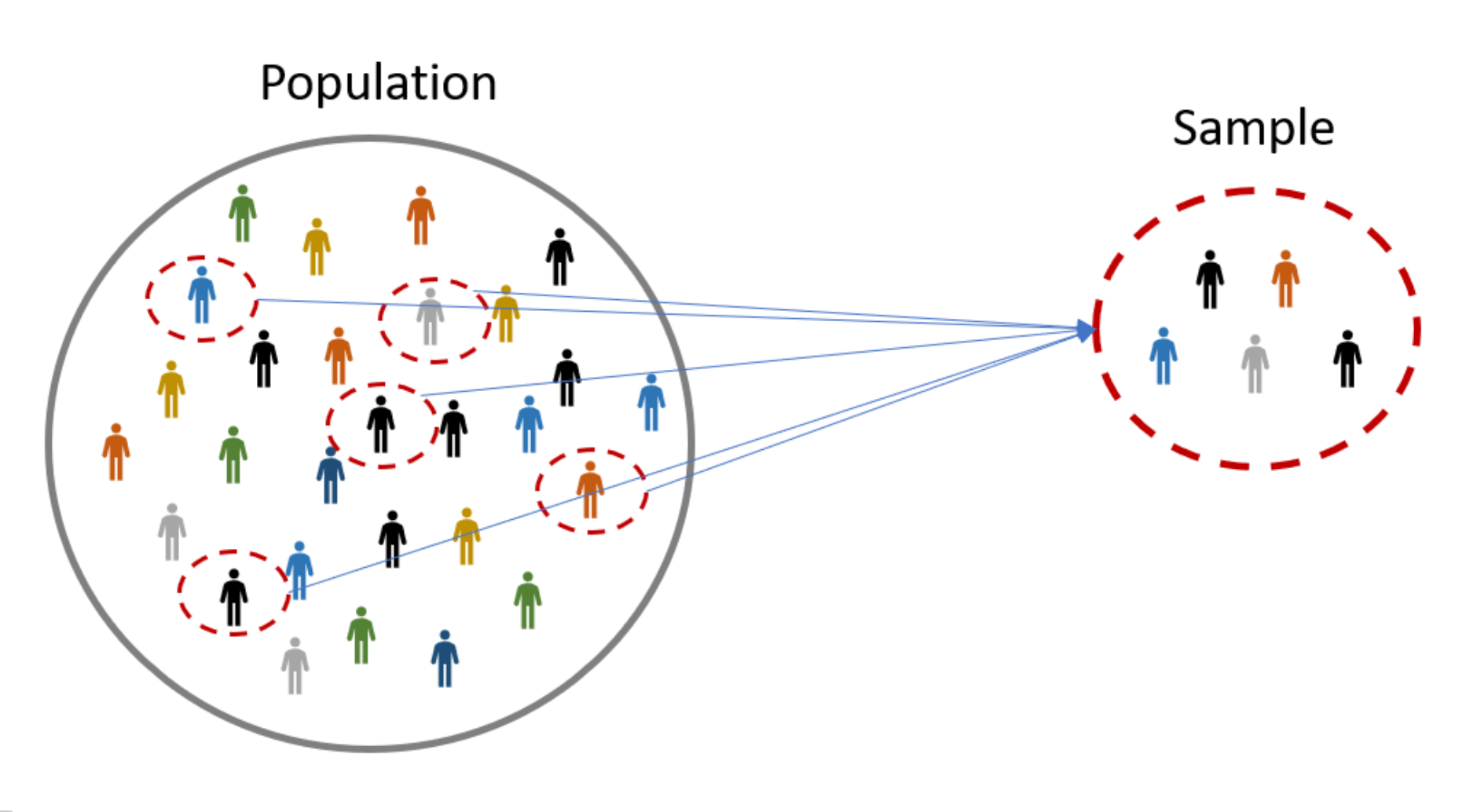
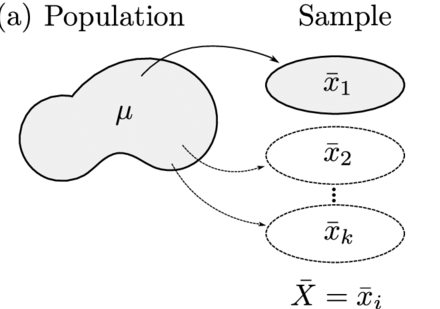
Muestra
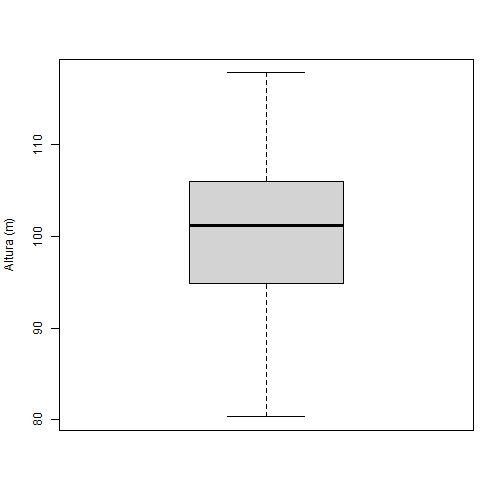
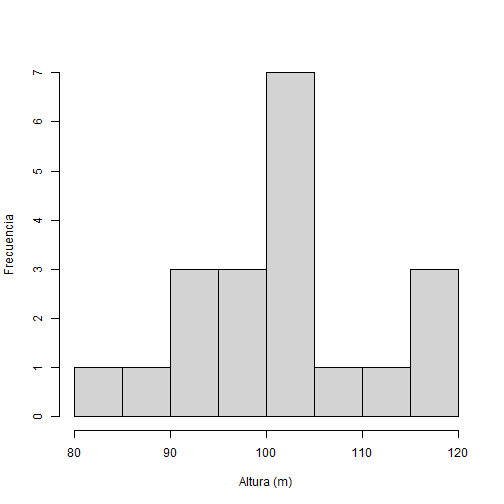
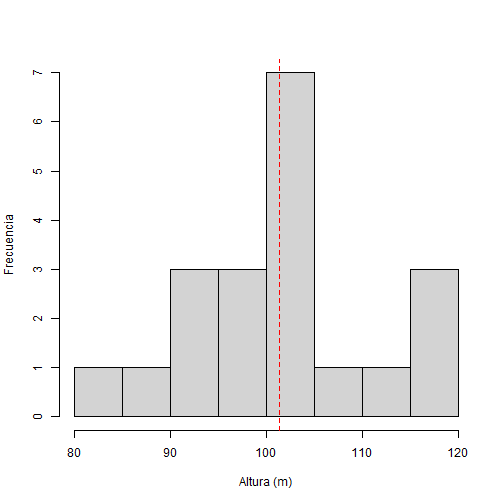
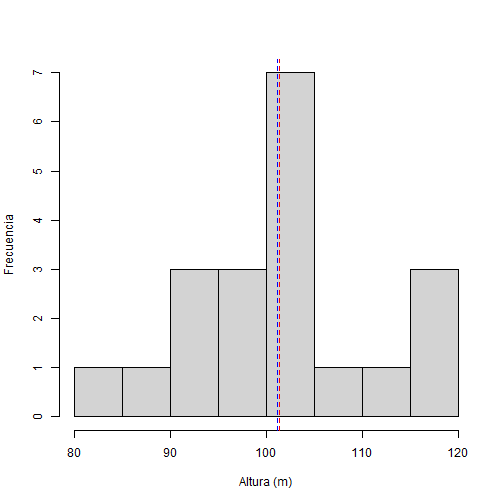
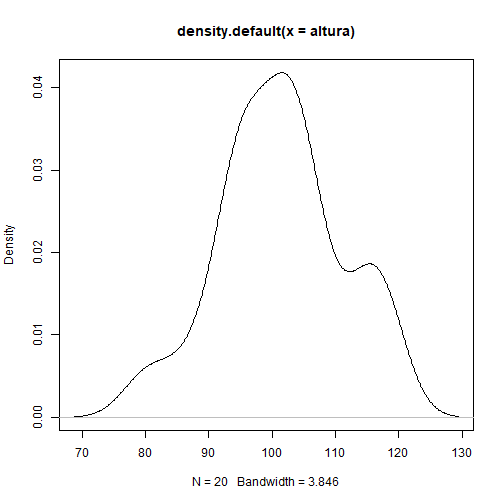
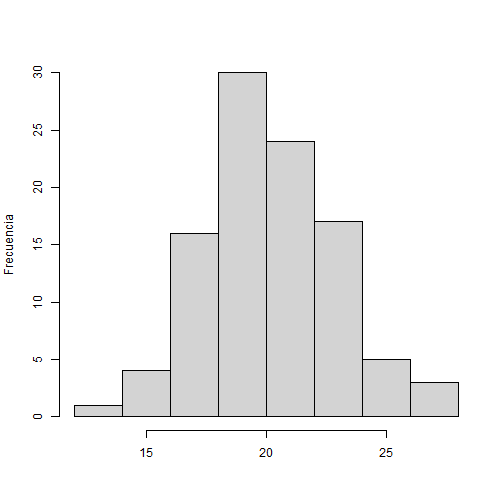
Tomamos datos de la altura ( m ) de 20 árboles ( n=20 ) de un bosque que se quiere investigar y lo guardamos en un vector llamado altura:
print(altura)## [1] 94.40 97.70 115.59 100.71 101.29 117.15 104.61 87.35 93.13 95.54## [11] 112.24 103.60 104.01 101.11 94.44 117.87 104.98 80.33 107.01 95.27--
También tomamos datos del número de raíces principales de cada árbol:
print(raices)## [1] 1 3 2 4 4 0 2 4 2 2 5 2 3 2 0 4 1 0 1 5Moda
El valor más frecuente en los datos.
R no tiene una función por defecto para calcular la moda, pero podemos hacer una:
getmode <- function(x) { uniqv <- unique(x) uniqv[which.max(tabulate(match(x, uniqv)))]}Luego la usamos:
getmode(x = raices)## [1] 2O utilizar:
DescTools::Mode(x = altura)Cuartiles y percentiles
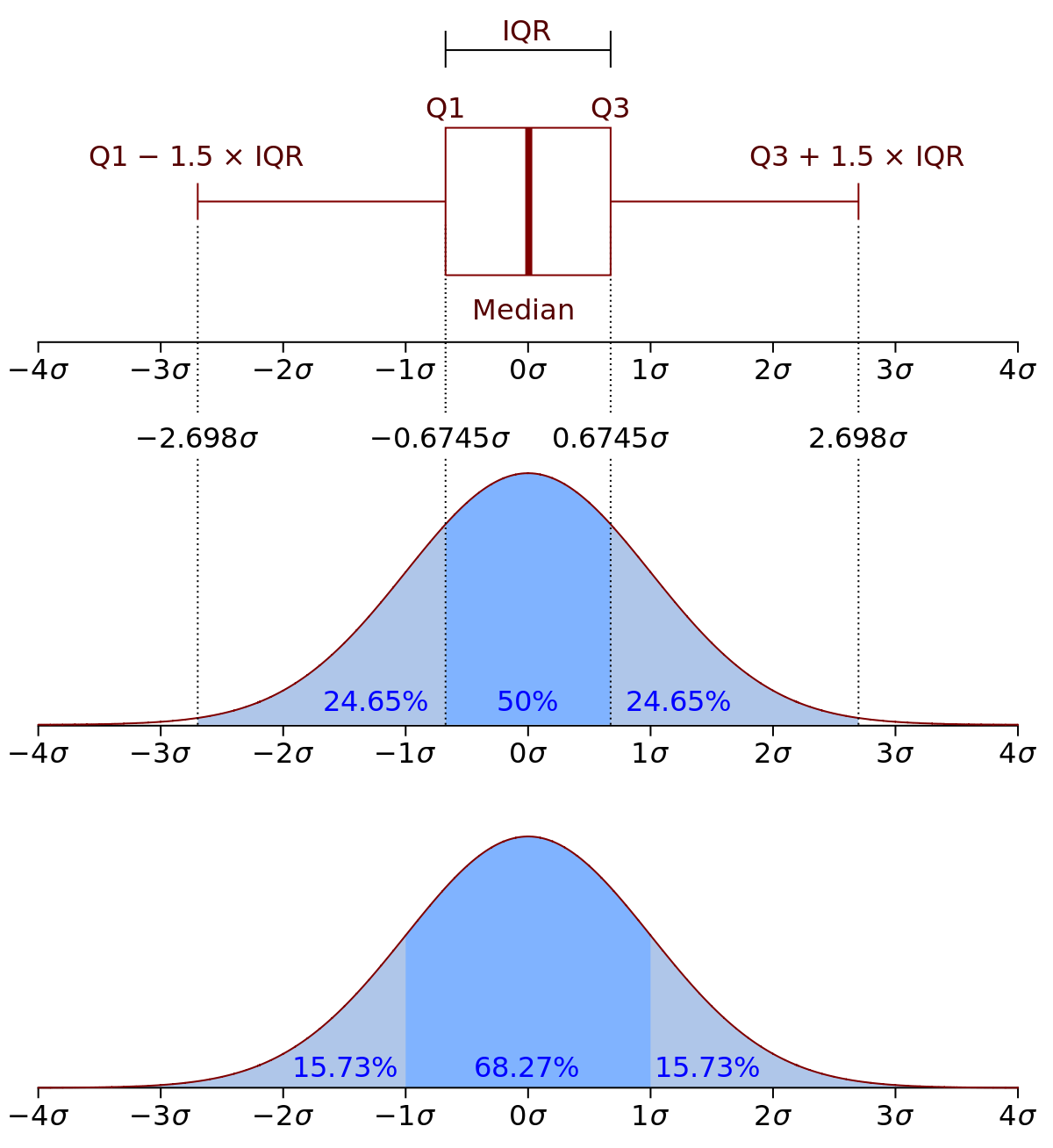
Cuartiles: Valores que dividen a los datos en cuatro partes. E.g.: primer (25%), segundo (50%) y tercer (75%) cuartil.
Percentil: Valores que dividen a los datos en cien partes. E.g.: Percentil 1, 2, etc.
En R podemos usar (para cuartiles y percentiles) (Unidades: m):
quantile(x = altura, probs = 0.25)## 25% ## 95.0625Aquí, probs = 0.25 especifica el primer cuartil o el percentil 25.
Cuartiles y percentiles
Cuartiles: Valores que dividen a los datos en cuatro partes. E.g.: primer (25%), segundo (50%) y tercer (75%) cuartil.
Percentil: Valores que dividen a los datos en cien partes. E.g.: Percentil 1, 2, etc.
En R podemos usar (para cuartiles y percentiles) (Unidades: m):
quantile(x = altura, probs = 0.25)## 25% ## 95.0625Aquí, probs = 0.25 especifica el primer cuartil o el percentil 25.
quantile(x = altura, probs = 0.6)## 60% ## 103.764Aquí, probs = 0.6 especifica el percentil 60.
Datos faltantes
En el caso que tengamos datos faltantes, la variable puede ser:
## [1] 94.40 97.70 NA 100.71 101.29 117.15 NA 87.35 93.13 95.54## [11] 112.24 103.60 104.01 101.11 94.44 117.87 104.98 80.33 107.01 95.27--
Si usamos las funciones anteriores tal cual, vemos que:
mean(altura)## [1] NADatos faltantes
En el caso que tengamos datos faltantes, la variable puede ser:
## [1] 94.40 97.70 NA 100.71 101.29 117.15 NA 87.35 93.13 95.54## [11] 112.24 103.60 104.01 101.11 94.44 117.87 104.98 80.33 107.01 95.27--
Si usamos las funciones anteriores tal cual, vemos que:
mean(altura)## [1] NAEn estos casos, tenemos que agregar el argumento na.rm = TRUE a las funciones exploradas:
mean(altura, na.rm = TRUE)## [1] 100.4517Resumen de un conjunto de datos
Podemos obtener estadísticos descriptivos rápidamente de todas las variables de una base de datos, por ejemplo:
summary(airquality)## Ozone Solar.R Wind Temp ## Min. : 1.00 Min. : 7.0 Min. : 1.700 Min. :56.00 ## 1st Qu.: 18.00 1st Qu.:115.8 1st Qu.: 7.400 1st Qu.:72.00 ## Median : 31.50 Median :205.0 Median : 9.700 Median :79.00 ## Mean : 42.13 Mean :185.9 Mean : 9.958 Mean :77.88 ## 3rd Qu.: 63.25 3rd Qu.:258.8 3rd Qu.:11.500 3rd Qu.:85.00 ## Max. :168.00 Max. :334.0 Max. :20.700 Max. :97.00 ## NA's :37 NA's :7 ## Month Day ## Min. :5.000 Min. : 1.0 ## 1st Qu.:6.000 1st Qu.: 8.0 ## Median :7.000 Median :16.0 ## Mean :6.993 Mean :15.8 ## 3rd Qu.:8.000 3rd Qu.:23.0 ## Max. :9.000 Max. :31.0 ##Distribuciones de probabilidad
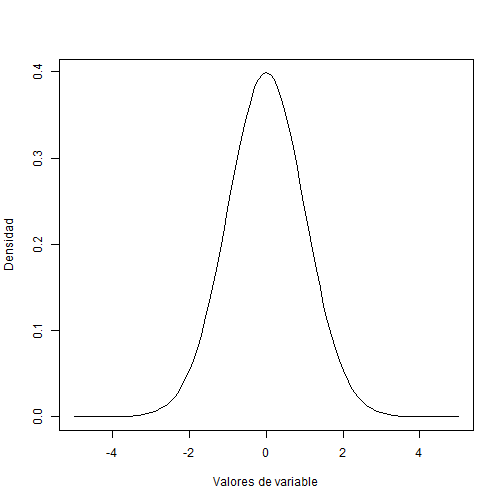
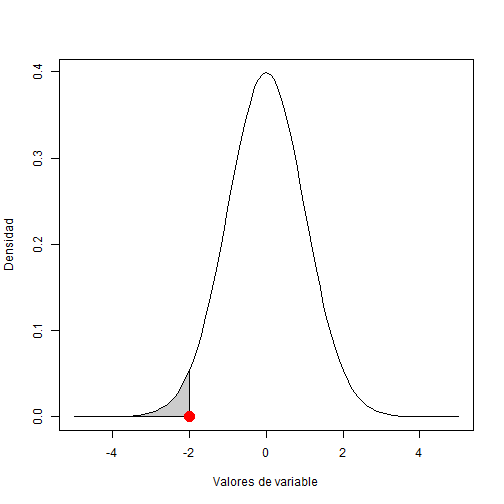
Distribución normal
Ejemplo 1:
¿Cúal es la probabilidad que la altura de un árbol sea menor a 90 m, dado que la media de la muestra es 100 y desviación estándar de 10?
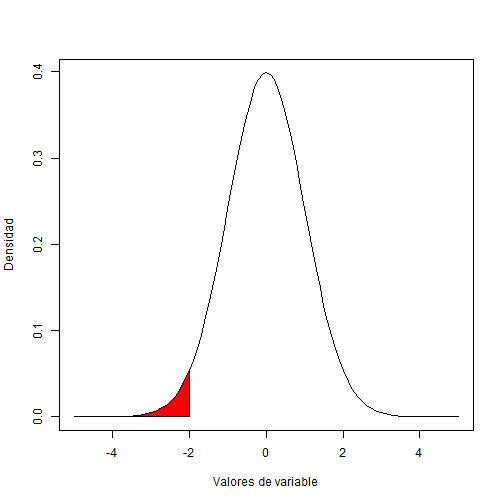
pnorm(q = 90, mean = 100, sd = 10)## [1] 0.1586553Ejemplo 2:
¿Cúal es la probabilidad que la altura de un árbol sea mayor a 115 m, dado que la media de la muestra es 100 y desviación estándar de 10?
Distribución normal
Ejemplo 1:
¿Cúal es la probabilidad que la altura de un árbol sea menor a 90 m, dado que la media de la muestra es 100 y desviación estándar de 10?
pnorm(q = 90, mean = 100, sd = 10)## [1] 0.1586553Ejemplo 2:
¿Cúal es la probabilidad que la altura de un árbol sea mayor a 115 m, dado que la media de la muestra es 100 y desviación estándar de 10?
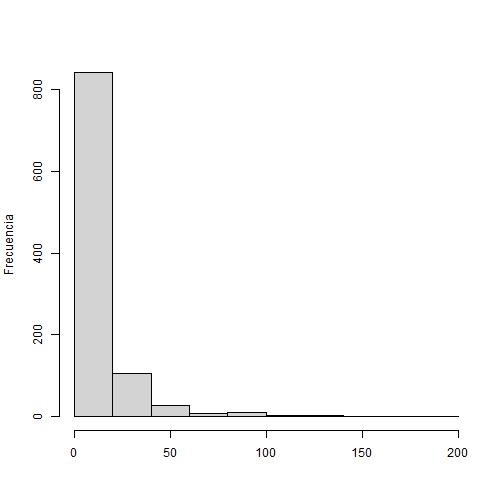
1 - pnorm(q = 115, mean = 100, sd = 10)## [1] 0.0668072Distribución lognormal
Similar al caso de la distribución normal, podemos calcular:
Probabilidad acumulada:
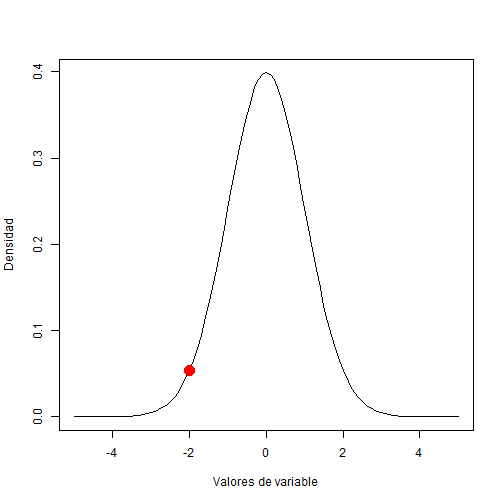
plnorm(q = 20, mean = 2, sd = 1)## [1] 0.8403099Probabilidad a un valor de variable dado:
dlnorm(x = 20, mean = 2, sd = 1)## [1] 0.01215017Valor de variable dado una probabilidad acumulada:
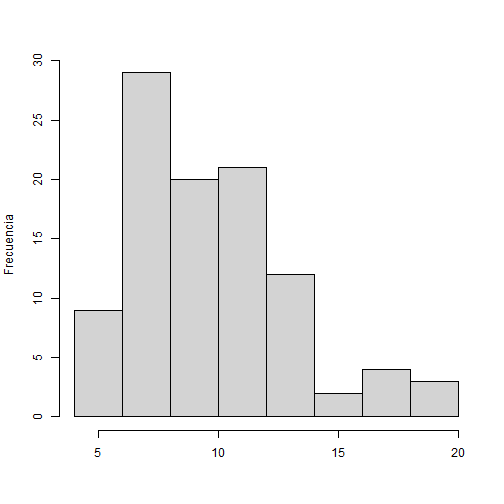
qlnorm(p = 0.84, mean = 2, sd = 1)## [1] 19.97453Distribución poisson
Similar al caso de la distribución normal, podemos calcular:
Probabilidad acumulada:
ppois(q = 8, lambda = 10)## [1] 0.3328197Probabilidad a un valor de variable dado:
dpois(x = 8, lambda = 10)## [1] 0.112599Valor de variable dado una probabilidad acumulada:
qpois(p = 0.33, lambda = 10)## [1] 8Distribución binomial
Podemos generar 100 experimentos (n=100), cada uno con 20 intentos (size=20), donde cada intento tiene probabilidad de éxito p=0.5 para un evento de interés:
rbinom(n = 100, size = 20, prob = 0.5)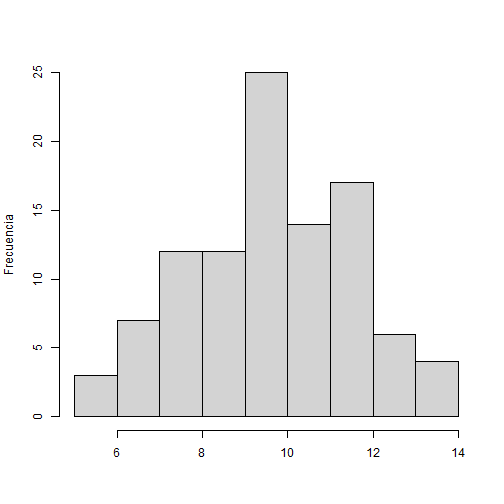
El número de veces donde el evento de interés ha sido exitoso para los 100 experimentos
Distribución binomial
Similar al caso de la distribución normal, podemos calcular:
Probabilidad acumulada:
pbinom(q = 10, size = 20, prob = 0.5)## [1] 0.5880985Probabilidad a un valor de variable dado:
dbinom(x = 10, size = 20, prob = 0.5)## [1] 0.1761971Valor de variable dado una probabilidad acumulada:
qbinom(p = 0.588, size = 20, prob = 0.5)## [1] 10