AlwaysR, Módulo III: Estadística en R
Clase 2: Pruebas de hipótesis. ANOVA. Comparaciones múltiples.
Dr. Giancarlo M. Correa

Pruebas de hipótesis
Prueba de hipótesis
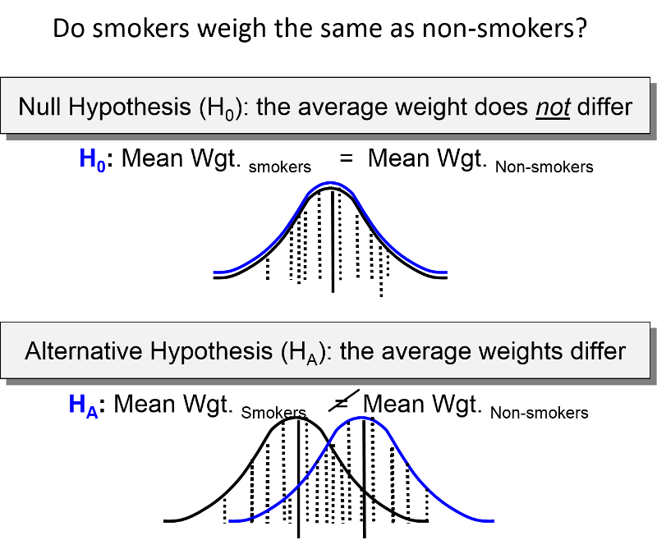
- Hipótesis nula ( \(H_0\) ): Un valor especificado o rango de valores para el parámetro de interés. Normalmente representa los valores ‘no interesantes’.
Ejemplo: \(H_0: \mu = 0\)
- Hipótesis alternativa ( \(H_A\) ): Un valor especificado diferente o rango de valores para el parámetro de interés. Normalmente representan los valores ‘interesantes’.
Ejemplo: \(H_A: \mu \neq 0\)
Componentes de una prueba de hipótesis
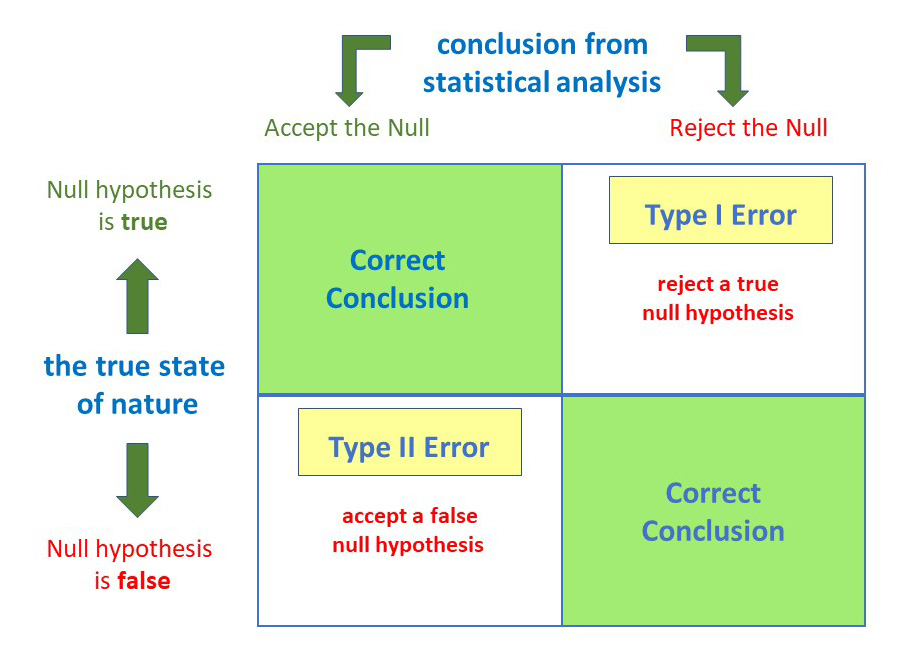
Nivel de significancia ( \(\alpha\) ): probabilidad de un error Tipo I (rechazar la hipótesis nula cuando de hecho es verdadera).
Estadístico de prueba: Valor calculado a partir de una función de los valores muestreados que es usado para decidir entre la hipótesis nula o alternativa.
Componentes de una prueba de hipótesis
Nivel de significancia ( \(\alpha\) ): probabilidad de un error Tipo I (rechazar la hipótesis nula cuando de hecho es verdadera).
Estadístico de prueba: Valor calculado a partir de una función de los valores muestreados que es usado para decidir entre la hipótesis nula o alternativa.
Distribución de referencia: Distribución que usamos para decidir si rechazamos la hipótesis nula.
Componentes de una prueba de hipótesis
Nivel de significancia ( \(\alpha\) ): probabilidad de un error Tipo I (rechazar la hipótesis nula cuando de hecho es verdadera).
Estadístico de prueba: Valor calculado a partir de una función de los valores muestreados que es usado para decidir entre la hipótesis nula o alternativa.
Distribución de referencia: Distribución que usamos para decidir si rechazamos la hipótesis nula.
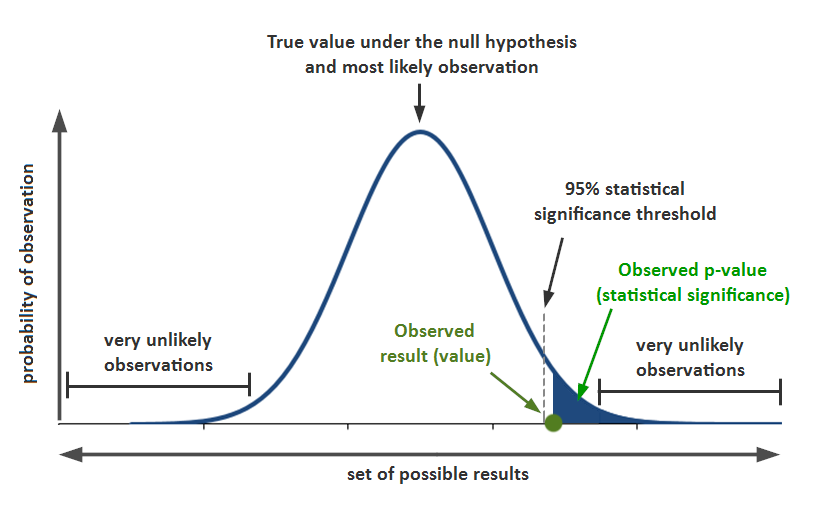
Región de rechazo: Valores para los cuales la hipótesis nula será rechazada.
Componentes de una prueba de hipótesis
Nivel de significancia ( \(\alpha\) ): probabilidad de un error Tipo I (rechazar la hipótesis nula cuando de hecho es verdadera).
Estadístico de prueba: Valor calculado a partir de una función de los valores muestreados que es usado para decidir entre la hipótesis nula o alternativa.
Distribución de referencia: Distribución que usamos para decidir si rechazamos la hipótesis nula.
Región de rechazo: Valores para los cuales la hipótesis nula será rechazada.
Valor crítico: Valor con el cual el estadístico de prueba será comparado para decidir si rechazamos la hipótesis nula.
Pruebas de hipótesis de una muestra
Prueba Z (Z-test)
Cuando conocemos la varianza poblacional.
Tenemos: \(H_0: \mu\leq \mu_0\) ó \(H_0: \mu\geq \mu_0\) ó \(H_0: \mu=\mu_0\)
Estadístico de prueba:
$$Z = \frac{\bar{X}-\mu_0}{\sqrt{\sigma^2/n}}$$
Se asume que la varianza de la población es conocida ( \(\sigma^2\) ). \(n\) es el individuos en la muestra. \(\bar{X}\) es la media de la muestra.
Prueba Z (Z-test)
Cuando conocemos la varianza poblacional.
Tenemos: \(H_0: \mu\leq \mu_0\) ó \(H_0: \mu\geq \mu_0\) ó \(H_0: \mu=\mu_0\)
Estadístico de prueba:
$$Z = \frac{\bar{X}-\mu_0}{\sqrt{\sigma^2/n}}$$
Se asume que la varianza de la población es conocida ( \(\sigma^2\) ). \(n\) es el individuos en la muestra. \(\bar{X}\) es la media de la muestra.
Distribución de referencia: \(Z \sim N(0,1)\)
Prueba Z (Z-test)
Cuando conocemos la varianza poblacional.
Tenemos: \(H_0: \mu\leq \mu_0\) ó \(H_0: \mu\geq \mu_0\) ó \(H_0: \mu=\mu_0\)
Estadístico de prueba:
$$Z = \frac{\bar{X}-\mu_0}{\sqrt{\sigma^2/n}}$$
Se asume que la varianza de la población es conocida ( \(\sigma^2\) ). \(n\) es el individuos en la muestra. \(\bar{X}\) es la media de la muestra.
Distribución de referencia: \(Z \sim N(0,1)\)
Decisión:
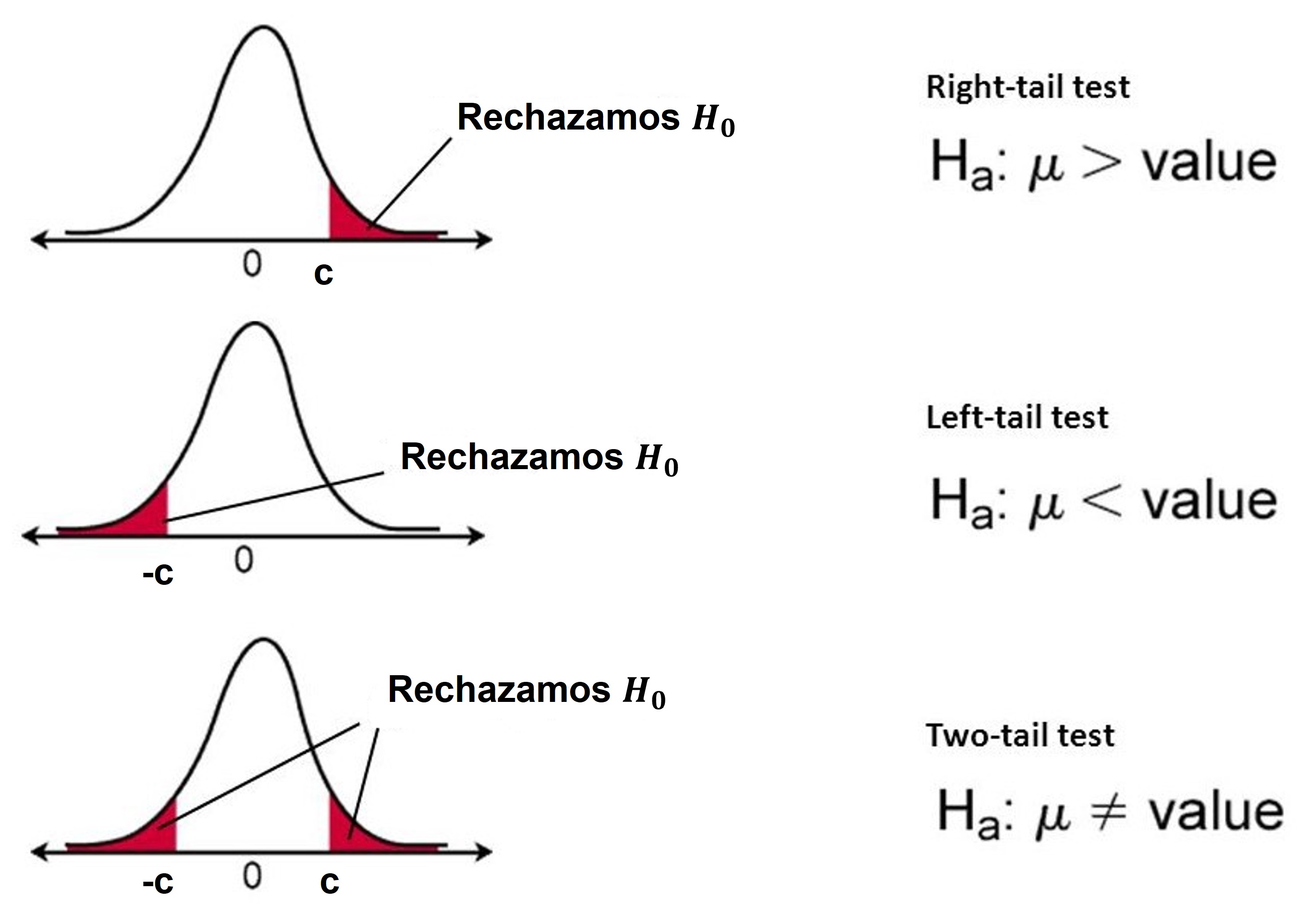
- \(H_A: \mu > \mu_0\): Rechazamos \(H_0\) cuando \(Z>z_{1-\alpha}\)
- \(H_A: \mu < \mu_0\): Rechazamos \(H_0\) cuando \(Z<z_{1-\alpha}\)
- \(H_A: \mu \neq \mu_0\): Rechazamos \(H_0\) cuando \(\mid Z\mid >z_{1-\alpha /2}\)
Prueba Z (Z-test)
Para:
- \(H_0: \mu = 0\)
- \(H_A: \mu \neq 0\)
- \(\sigma = 0.4\)
En R podemos usar (librería BSDA):
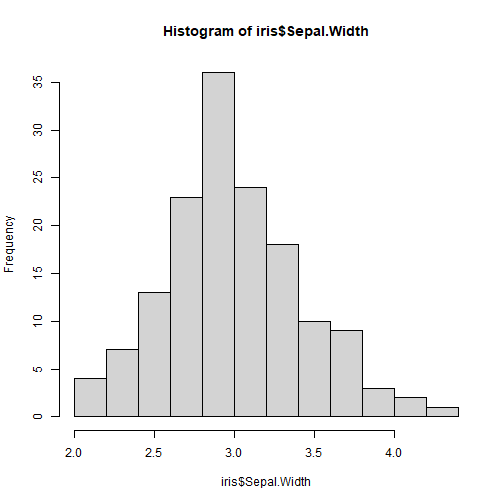
z.test(x = iris$Sepal.Width, alternative = 'two.sided', mu = 0, sigma.x = 0.4)## ## One-sample z-Test## ## data: iris$Sepal.Width## z = 93.611, p-value < 2.2e-16## alternative hypothesis: true mean is not equal to 0## 95 percent confidence interval:## 2.993321 3.121345## sample estimates:## mean of x ## 3.057333Intervalos de confianza
El intervalo construido contendrá el valor verdadero de \(\mu\) (media de la población) el \((1-\alpha)100\%\) de las veces que repetimos el experimento.
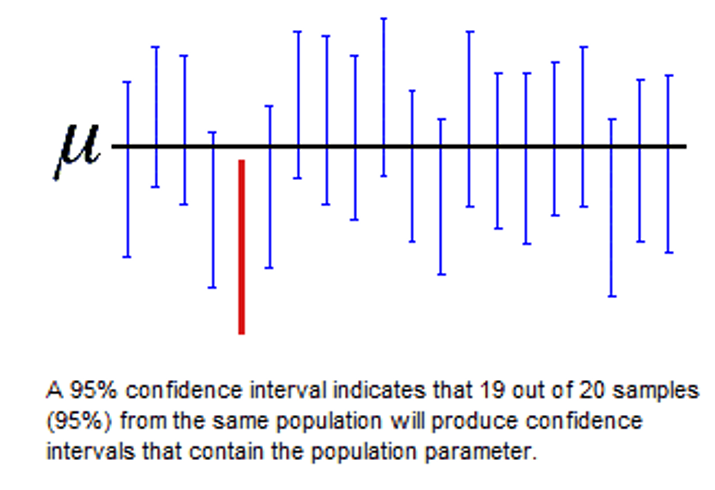
- NO es correcto decir que hay \((1-\alpha)100\%\) de probabilidad que la media de la población este en este intervalo (de un experimento en específico).
Prueba Z (Z-test)
Para:
- \(H_0: \mu \geq 0\)
- \(H_A: \mu < 0\)
- \(\sigma = 0.4\)
En R podemos usar (librería BSDA):
z.test(x = iris$Sepal.Width, alternative = 'less', mu = 0, sigma.x = 0.4)## ## One-sample z-Test## ## data: iris$Sepal.Width## z = 93.611, p-value = 1## alternative hypothesis: true mean is less than 0## 95 percent confidence interval:## NA 3.111054## sample estimates:## mean of x ## 3.057333Prueba Z (Z-test)
Para:
- \(H_0: \mu \leq 0\)
- \(H_A: \mu > 0\)
- \(\sigma = 0.4\)
En R podemos usar (librería BSDA):
z.test(x = iris$Sepal.Width, alternative = 'greater', mu = 0, sigma.x = 0.4)## ## One-sample z-Test## ## data: iris$Sepal.Width## z = 93.611, p-value < 2.2e-16## alternative hypothesis: true mean is greater than 0## 95 percent confidence interval:## 3.003613 NA## sample estimates:## mean of x ## 3.057333Prueba t (t-test)
Cuando no conocemos la varianza poblacional pero si la muestral.
Tenemos: \(H_0: \mu\leq \mu_0\) ó \(H_0: \mu\geq \mu_0\) ó \(H_0: \mu=\mu_0\)
Estadístico de prueba:
$$t = \frac{\bar{X}-\mu_0}{\sqrt{s^2/n}}$$
\(n\) es el individuos en la muestra. \(\bar{X}\) es la media de la muestra. \(s^2\) es la varianza muestral.
Prueba t (t-test)
Cuando no conocemos la varianza poblacional pero si la muestral.
Tenemos: \(H_0: \mu\leq \mu_0\) ó \(H_0: \mu\geq \mu_0\) ó \(H_0: \mu=\mu_0\)
Estadístico de prueba:
$$t = \frac{\bar{X}-\mu_0}{\sqrt{s^2/n}}$$
\(n\) es el individuos en la muestra. \(\bar{X}\) es la media de la muestra. \(s^2\) es la varianza muestral.
Distribución de referencia: \(t \sim t_{n-1}\)
Prueba t (t-test)
Cuando no conocemos la varianza poblacional pero si la muestral.
Tenemos: \(H_0: \mu\leq \mu_0\) ó \(H_0: \mu\geq \mu_0\) ó \(H_0: \mu=\mu_0\)
Estadístico de prueba:
$$t = \frac{\bar{X}-\mu_0}{\sqrt{s^2/n}}$$
\(n\) es el individuos en la muestra. \(\bar{X}\) es la media de la muestra. \(s^2\) es la varianza muestral.
Distribución de referencia: \(t \sim t_{n-1}\)
Decisión:
- \(H_A: \mu > \mu_0\): Rechazamos \(H_0\) cuando \(t>t_{n-1,1-\alpha}\)
- \(H_A: \mu < \mu_0\): Rechazamos \(H_0\) cuando \(t<t_{n-1,\alpha}\)
- \(H_A: \mu \neq \mu_0\): Rechazamos \(H_0\) cuando \(\mid t\mid >t_{n-1,1-\alpha /2}\)
Prueba t (t-test)
Para:
- \(H_0: \mu = 0\)
- \(H_A: \mu \neq 0\)
En R podemos usar:
t.test(x = iris$Sepal.Width, alternative = 'two.sided', mu = 0)## ## One Sample t-test## ## data: iris$Sepal.Width## t = 85.908, df = 149, p-value < 2.2e-16## alternative hypothesis: true mean is not equal to 0## 95 percent confidence interval:## 2.987010 3.127656## sample estimates:## mean of x ## 3.057333Prueba binomial (exacta)
Ejemplo:
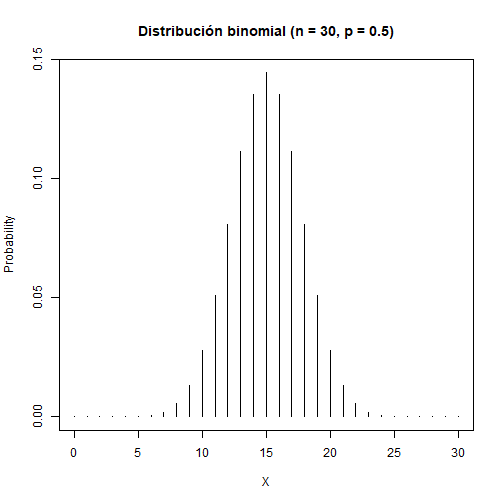
Supongamos que realizo un muestreo de una población y capturé 30 individuos ( \(n=30\) ). El evento de interés es que un individuo sea macho ( \(p = P(macho)\) ). Tenemos que \(H_0: p\leq 0.5\) y \(H_A: p>0.5\). Entonces:
- Si observo \(X = 5\) machos, debo rechazar \(H_0\)?
Prueba binomial (exacta)
Ejemplo:
Supongamos que realizo un muestreo de una población y capturé 30 individuos ( \(n=30\) ). El evento de interés es que un individuo sea macho ( \(p = P(macho)\) ). Tenemos que \(H_0: p\leq 0.5\) y \(H_A: p>0.5\). Entonces:
Si observo \(X = 5\) machos, debo rechazar \(H_0\)?
Si observo \(X = 15\) machos, debo rechazar \(H_0\)?
Prueba binomial (exacta)
Ejemplo:
Supongamos que realizo un muestreo de una población y capturé 30 individuos ( \(n=30\) ). El evento de interés es que un individuo sea macho ( \(p = P(macho)\) ). Tenemos que \(H_0: p\leq 0.5\) y \(H_A: p>0.5\). Entonces:
Si observo \(X = 5\) machos, debo rechazar \(H_0\)?
Si observo \(X = 15\) machos, debo rechazar \(H_0\)?
Si observo \(X = 25\) machos, debo rechazar \(H_0\)?
Prueba binomial (exacta)
Tenemos: \(H_0: p\leq p_0\) ó \(H_0: p\geq p_0\) ó \(H_0: p=p_0\)
Distribución de referencia: \(X \sim Binom(n,p_0)\)
Donde \(X = \sum_{i=1}^n Y_i\), e \(Y_i\) es un evento con éxito/fracaso:
$$P(Y_i=1)=p\hspace{3cm}P(Y_i=0)=1-p$$
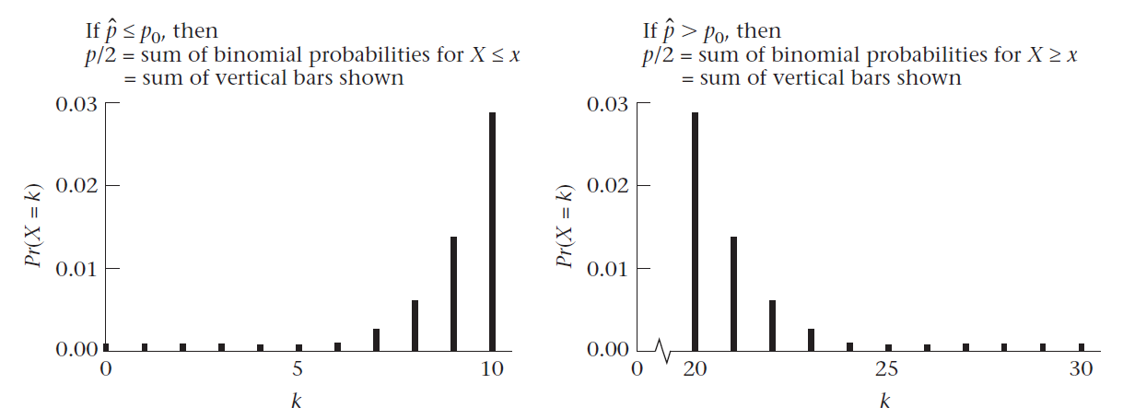
Decisión:
- \(H_A: p > p_0\): Rechazamos \(H_0\) cuando?
- \(H_A: p < p_0\): Rechazamos \(H_0\) cuando?
- \(H_A: p \neq p_0\): Rechazamos \(H_0\) cuando?
Prueba binomial (exacta)
- \(H_0: p = 0.5\)
- \(H_A: p \neq 0.5\)
En R podemos usar:
binom.test(x = X, n = n, p = 0.5, alternative = 'two.sided')## ## Exact binomial test## ## data: X and n## number of successes = 50, number of trials = 150, p-value = 5.448e-05## alternative hypothesis: true probability of success is not equal to 0.5## 95 percent confidence interval:## 0.2585564 0.4148430## sample estimates:## probability of success ## 0.3333333Prueba Kolmogorov-Smirnov
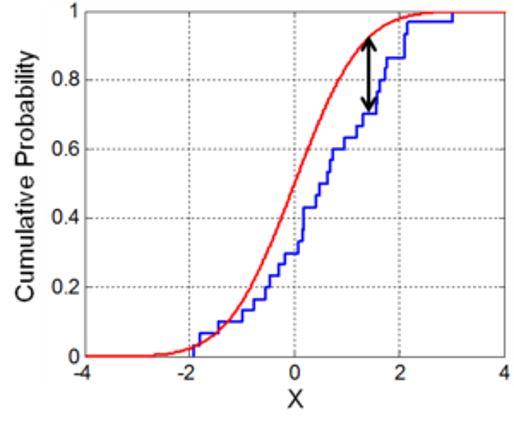
En R podemos usar:
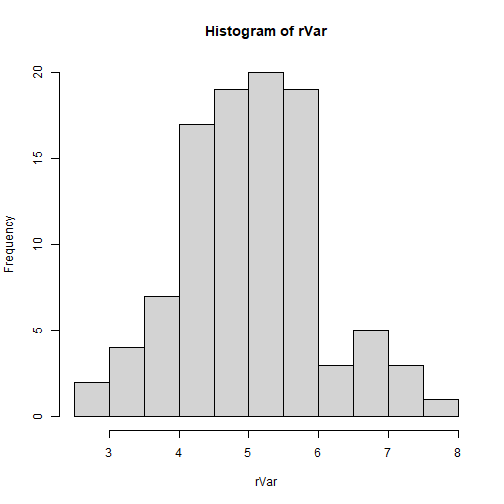
ks.test(x = rVar, y = 'pnorm', mean = 3, sd = 0.4, alternative = 'two.sided')## ## Asymptotic one-sample Kolmogorov-Smirnov test## ## data: rVar## D = 0.89207, p-value < 2.2e-16## alternative hypothesis: two-sidedEn este caso:
- \(H_0: F(x) = N(3,0.4^2)\)
- \(H_A: F(x) \neq N(3,0.4^2)\)
Pruebas de hipótesis de dos muestras
Prueba t de muestras independientes
Tenemos: \(H_0: \delta\leq \delta_0\) ó \(H_0: \delta\geq \delta_0\) ó \(H_0: \delta=\delta_0\)
Donde: \(\delta = \mu_X-\mu_Y\)
Estadístico de prueba:
$$t = \frac{\hat{\delta}-\delta_0}{\sqrt{s_p^2/m + s_p^2/n}}$$
\(m\) es el número de individuos en la muestra 1 y \(n\) es el número de individuos en la muestra 2. \(\bar{X}\) es la media de la muestra. \(s_p^2\) es la varianza agrupada. \(\hat{\delta} = \bar{X}-\bar{Y}\).
Prueba t de muestras independientes
Tenemos: \(H_0: \delta\leq \delta_0\) ó \(H_0: \delta\geq \delta_0\) ó \(H_0: \delta=\delta_0\)
Donde: \(\delta = \mu_X-\mu_Y\)
Estadístico de prueba:
$$t = \frac{\hat{\delta}-\delta_0}{\sqrt{s_p^2/m + s_p^2/n}}$$
\(m\) es el número de individuos en la muestra 1 y \(n\) es el número de individuos en la muestra 2. \(\bar{X}\) es la media de la muestra. \(s_p^2\) es la varianza agrupada. \(\hat{\delta} = \bar{X}-\bar{Y}\).
Distribución de referencia: \(t \sim t_{m+n-2}\)
Prueba t de muestras independientes
Tenemos: \(H_0: \delta\leq \delta_0\) ó \(H_0: \delta\geq \delta_0\) ó \(H_0: \delta=\delta_0\)
Donde: \(\delta = \mu_X-\mu_Y\)
Estadístico de prueba:
$$t = \frac{\hat{\delta}-\delta_0}{\sqrt{s_p^2/m + s_p^2/n}}$$
\(m\) es el número de individuos en la muestra 1 y \(n\) es el número de individuos en la muestra 2. \(\bar{X}\) es la media de la muestra. \(s_p^2\) es la varianza agrupada. \(\hat{\delta} = \bar{X}-\bar{Y}\).
Distribución de referencia: \(t \sim t_{m+n-2}\)
Decisión:
- \(H_A: \delta > \delta_0\): Rechazamos \(H_0\) cuando \(t>t_{m+n-2,1-\alpha}\)
- \(H_A: \delta < \delta_0\): Rechazamos \(H_0\) cuando \(t<t_{m+n-2,\alpha}\)
- \(H_A: \delta \neq \delta_0\): Rechazamos \(H_0\) cuando \(\mid t\mid >t_{m+n-2,1-\alpha /2}\)
Prueba t de muestras independientes
Y en R podemos usar la función:
t.test(x = setosaVal, y = virginicaVal, alternative = 'two.sided', mu = 0, paired = FALSE, var.equal = FALSE)## ## Welch Two Sample t-test## ## data: setosaVal and virginicaVal## t = -49.986, df = 58.609, p-value < 2.2e-16## alternative hypothesis: true difference in means is not equal to 0## 95 percent confidence interval:## -4.253749 -3.926251## sample estimates:## mean of x mean of y ## 1.462 5.552Prueba t de muestras independientes
Y en R podemos usar la función:
t.test(x = setosaVal, y = virginicaVal, alternative = 'two.sided', mu = 0, paired = FALSE, var.equal = FALSE)## ## Welch Two Sample t-test## ## data: setosaVal and virginicaVal## t = -49.986, df = 58.609, p-value < 2.2e-16## alternative hypothesis: true difference in means is not equal to 0## 95 percent confidence interval:## -4.253749 -3.926251## sample estimates:## mean of x mean of y ## 1.462 5.552- \(H_0: \delta = 0\)
- \(H_A: \delta \neq 0\)
Prueba t de muestras independientes
Y en R podemos usar la función:
t.test(x = setosaVal, y = virginicaVal, alternative = 'two.sided', mu = 0, paired = FALSE, var.equal = FALSE)## ## Welch Two Sample t-test## ## data: setosaVal and virginicaVal## t = -49.986, df = 58.609, p-value < 2.2e-16## alternative hypothesis: true difference in means is not equal to 0## 95 percent confidence interval:## -4.253749 -3.926251## sample estimates:## mean of x mean of y ## 1.462 5.552- \(H_0: \delta = 0\)
- \(H_A: \delta \neq 0\)
Tener cuidado al especificar los argumentos paired y var.equal.
Prueba t de muestras emparejadas
Tenemos: \(H_0: \delta\leq \delta_0\) ó \(H_0: \delta\geq \delta_0\) ó \(H_0: \delta=\delta_0\)
Donde: \(\delta = \mu_X-\mu_Y\)
Estadístico de prueba:
$$t = \frac{\hat{D}-\delta_0}{\sqrt{(s_x^2+s_y^2-2s_{xy})/n}}$$
\(n\) es el número de individuos en la muestra. \(s_{x}^2\) es la varianza muestral de grupo \(x\) y \(s_{y}^2\) del grupo \(y\). \(\hat{D} = \bar{X}-\bar{Y}\).
Prueba t de muestras emparejadas
Tenemos: \(H_0: \delta\leq \delta_0\) ó \(H_0: \delta\geq \delta_0\) ó \(H_0: \delta=\delta_0\)
Donde: \(\delta = \mu_X-\mu_Y\)
Estadístico de prueba:
$$t = \frac{\hat{D}-\delta_0}{\sqrt{(s_x^2+s_y^2-2s_{xy})/n}}$$
\(n\) es el número de individuos en la muestra. \(s_{x}^2\) es la varianza muestral de grupo \(x\) y \(s_{y}^2\) del grupo \(y\). \(\hat{D} = \bar{X}-\bar{Y}\).
Distribución de referencia: \(t \sim t_{n-1}\)
Prueba t de muestras emparejadas
Tenemos: \(H_0: \delta\leq \delta_0\) ó \(H_0: \delta\geq \delta_0\) ó \(H_0: \delta=\delta_0\)
Donde: \(\delta = \mu_X-\mu_Y\)
Estadístico de prueba:
$$t = \frac{\hat{D}-\delta_0}{\sqrt{(s_x^2+s_y^2-2s_{xy})/n}}$$
\(n\) es el número de individuos en la muestra. \(s_{x}^2\) es la varianza muestral de grupo \(x\) y \(s_{y}^2\) del grupo \(y\). \(\hat{D} = \bar{X}-\bar{Y}\).
Distribución de referencia: \(t \sim t_{n-1}\)
Decisión:
- \(H_A: \delta > \delta_0\): Rechazamos \(H_0\) cuando \(t>t_{n-1,1-\alpha}\)
- \(H_A: \delta < \delta_0\): Rechazamos \(H_0\) cuando \(t<t_{n-1,\alpha}\)
- \(H_A: \delta \neq \delta_0\): Rechazamos \(H_0\) cuando \(\mid t\mid >t_{n-1,1-\alpha /2}\)
Prueba t de muestras emparejadas
En R podemos usar la función:
t.test(x = BloodLead$Exposed, y = BloodLead$Control, alternative = 'two.sided', mu = 0, paired = TRUE)## ## Paired t-test## ## data: BloodLead$Exposed and BloodLead$Control## t = 5.783, df = 32, p-value = 2.036e-06## alternative hypothesis: true mean difference is not equal to 0## 95 percent confidence interval:## 10.34469 21.59470## sample estimates:## mean difference ## 15.9697Prueba t de muestras emparejadas
En R podemos usar la función:
t.test(x = BloodLead$Exposed, y = BloodLead$Control, alternative = 'two.sided', mu = 0, paired = TRUE)## ## Paired t-test## ## data: BloodLead$Exposed and BloodLead$Control## t = 5.783, df = 32, p-value = 2.036e-06## alternative hypothesis: true mean difference is not equal to 0## 95 percent confidence interval:## 10.34469 21.59470## sample estimates:## mean difference ## 15.9697- \(H_0: \delta = 0\)
- \(H_A: \delta \neq 0\)
Pruebas no paramétricas
Prueba Wilcoxon Signed-Rank
Utilizado cuando tenemos observaciones emparejadas y no tenemos información para asumir una distribución normal de la variable. Usando esta prueba podemos decidir si las distribuciones de los datos comparados son idénticas.
Usemos la base de datos:
library(MASS)head(immer)## Loc Var Y1 Y2## 1 UF M 81.0 80.7## 2 UF S 105.4 82.3## 3 UF V 119.7 80.4## 4 UF T 109.7 87.2## 5 UF P 98.3 84.2## 6 W M 146.6 100.4Pruebas no paramétricas
Prueba Wilcoxon Signed-Rank
En R podemos usar:
wilcox.test(x = immer$Y1, y = immer$Y2, paired=TRUE)## Warning in wilcox.test.default(x = immer$Y1, y = immer$Y2, paired = TRUE):## cannot compute exact p-value with ties## ## Wilcoxon signed rank test with continuity correction## ## data: immer$Y1 and immer$Y2## V = 368.5, p-value = 0.005318## alternative hypothesis: true location shift is not equal to 0- \(H_0:\) las distribuciones son idénticas
- \(H_A:\) las distribuciones no son idénticas
Pruebas no paramétricas
Prueba Mann-Whitney-Wilcoxon
Utilizado cuando tenemos observaciones independientes y no tenemos información para asumir una distribución normal de la variable. Usando esta prueba podemos decidir si las distribuciones de los datos comparados son idénticas.
Usemos la base de datos:
head(mtcars)## mpg cyl disp hp drat wt qsec vs am gear carb## Mazda RX4 21.0 6 160 110 3.90 2.620 16.46 0 1 4 4## Mazda RX4 Wag 21.0 6 160 110 3.90 2.875 17.02 0 1 4 4## Datsun 710 22.8 4 108 93 3.85 2.320 18.61 1 1 4 1## Hornet 4 Drive 21.4 6 258 110 3.08 3.215 19.44 1 0 3 1## Hornet Sportabout 18.7 8 360 175 3.15 3.440 17.02 0 0 3 2## Valiant 18.1 6 225 105 2.76 3.460 20.22 1 0 3 1Pruebas no paramétricas
Prueba Mann-Whitney-Wilcoxon
En R podemos usar:
wilcox.test(mpg ~ am, data=mtcars, paired = FALSE)## Warning in wilcox.test.default(x = DATA[[1L]], y = DATA[[2L]], ...): cannot## compute exact p-value with ties## ## Wilcoxon rank sum test with continuity correction## ## data: mpg by am## W = 42, p-value = 0.001871## alternative hypothesis: true location shift is not equal to 0- \(H_0:\) las distribuciones son idénticas
- \(H_A:\) las distribuciones no son idénticas
Pruebas no paramétricas
Prueba Kruskal-Wallis
Utilizado cuando tenemos observaciones independientes y no tenemos información para asumir una distribución normal de la variable. Usando esta prueba podemos decidir si las distribuciones de los datos comparados son idénticas.
Usemos la base de datos:
head(airquality)## Ozone Solar.R Wind Temp Month Day## 1 41 190 7.4 67 5 1## 2 36 118 8.0 72 5 2## 3 12 149 12.6 74 5 3## 4 18 313 11.5 62 5 4## 5 NA NA 14.3 56 5 5## 6 28 NA 14.9 66 5 6Pruebas no paramétricas
Prueba Kruskal-Wallis
En R podemos usar:
kruskal.test(Ozone ~ Month, data = airquality)## ## Kruskal-Wallis rank sum test## ## data: Ozone by Month## Kruskal-Wallis chi-squared = 29.267, df = 4, p-value = 6.901e-06- \(H_0:\) las distribuciones son idénticas
- \(H_A:\) las distribuciones no son idénticas
Prueba Chi-cuadrado de Pearson
En R podemos usar:
chisq.test(x = myTab)## ## Pearson's Chi-squared test with Yates' continuity correction## ## data: myTab## X-squared = 10.028, df = 1, p-value = 0.001542- \(H_0:\) las variables son independientes entre ellas
- \(H_A:\) las variables no son independientes entre ellas
Análisis de Varianza (ANOVA)
ANOVA
Tenemos varias muestras de diferentes poblaciones:
Muestra 1: \(X_{11}, ..., X_{1n_1}\) de la población 1 con media \(\mu_1\) y varianza \(\sigma_1^2\).
Muestra 2: \(X_{21}, ..., X_{2n_2}\) de la población 2 con media \(\mu_2\) y varianza \(\sigma_2^2\).
Muestra m: \(X_{m1}, ..., X_{mn_m}\) de la población m con media \(\mu_m\) y varianza \(\sigma_m^2\).
ANOVA
La pregunta al usar un ANOVA es: ¿Son las medias poblacionales iguales una con otra?
Por lo tanto, la hipótesis nula es:
\(H_0: \mu_1=\mu_2=...=\mu_m\)
La hipótesis alternativa es:
\(H_A: \mu_1\neq \mu_2\neq...\neq \mu_m\)
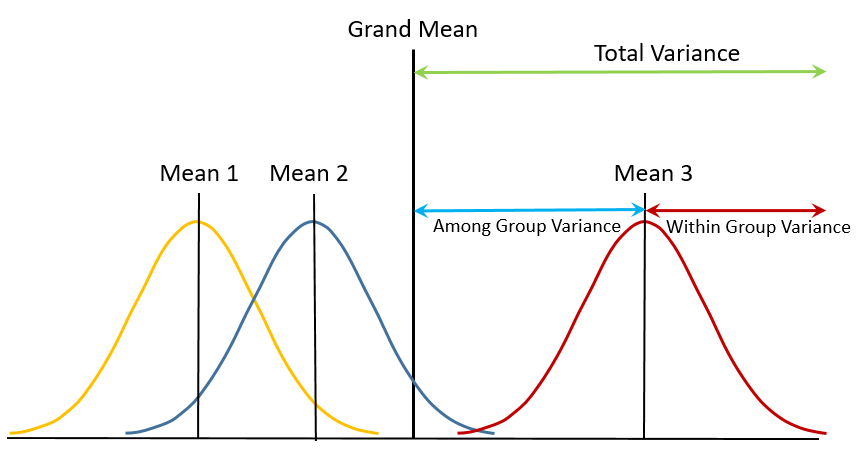
En palabras sencillas, un ANOVA compara la varianza dentro de los grupos con la varianza de todas las observaciones juntas para decidir si las medias poblacionales son iguales (es por esto que es llamado análisis de varianza).
ANOVA
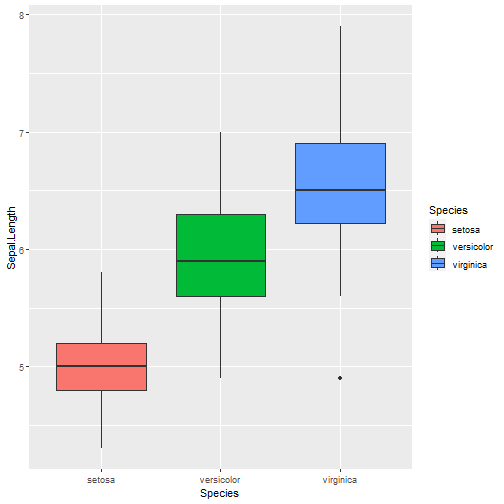
Hagamos un ANOVA para la variable seleccionada:
myAnova = aov(Sepal.Length ~ Species, data = iris)summary(myAnova)## Df Sum Sq Mean Sq F value Pr(>F) ## Species 2 63.21 31.606 119.3 <2e-16 ***## Residuals 147 38.96 0.265 ## ---## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Comparaciones de pares múltiples
Un ANOVA nos dice si alguna media es diferente, pero no nos dice cuál.
Si queremos comparar medias por pares, podemos usar una prueba Tukey.
Prueba Tukey
TukeyHSD(x = myAnova)## Tukey multiple comparisons of means## 95% family-wise confidence level## ## Fit: aov(formula = Sepal.Length ~ Species, data = iris)## ## $Species## diff lwr upr p adj## versicolor-setosa 0.930 0.6862273 1.1737727 0## virginica-setosa 1.582 1.3382273 1.8257727 0## virginica-versicolor 0.652 0.4082273 0.8957727 0ANOVA
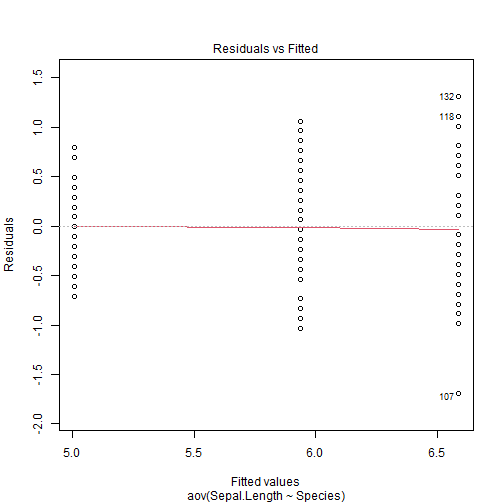
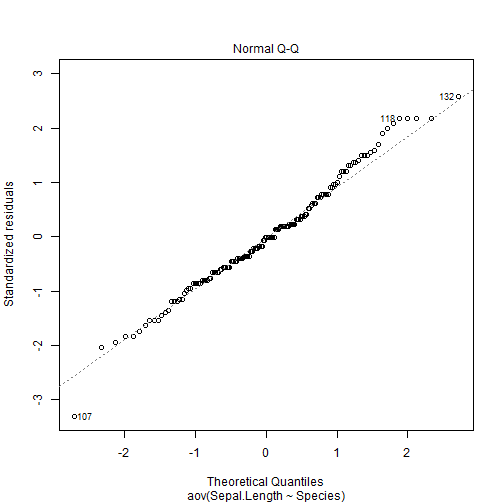
Homogeneidad de varianza
library(car)leveneTest(y = myAnova)## Levene's Test for Homogeneity of Variance (center = median)## Df F value Pr(>F) ## group 2 6.3527 0.002259 **## 147 ## ---## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1- \(H_0\): varianzas son iguales (homogéneas)
- \(H_A\): varianzas no son iguales (homogéneas)