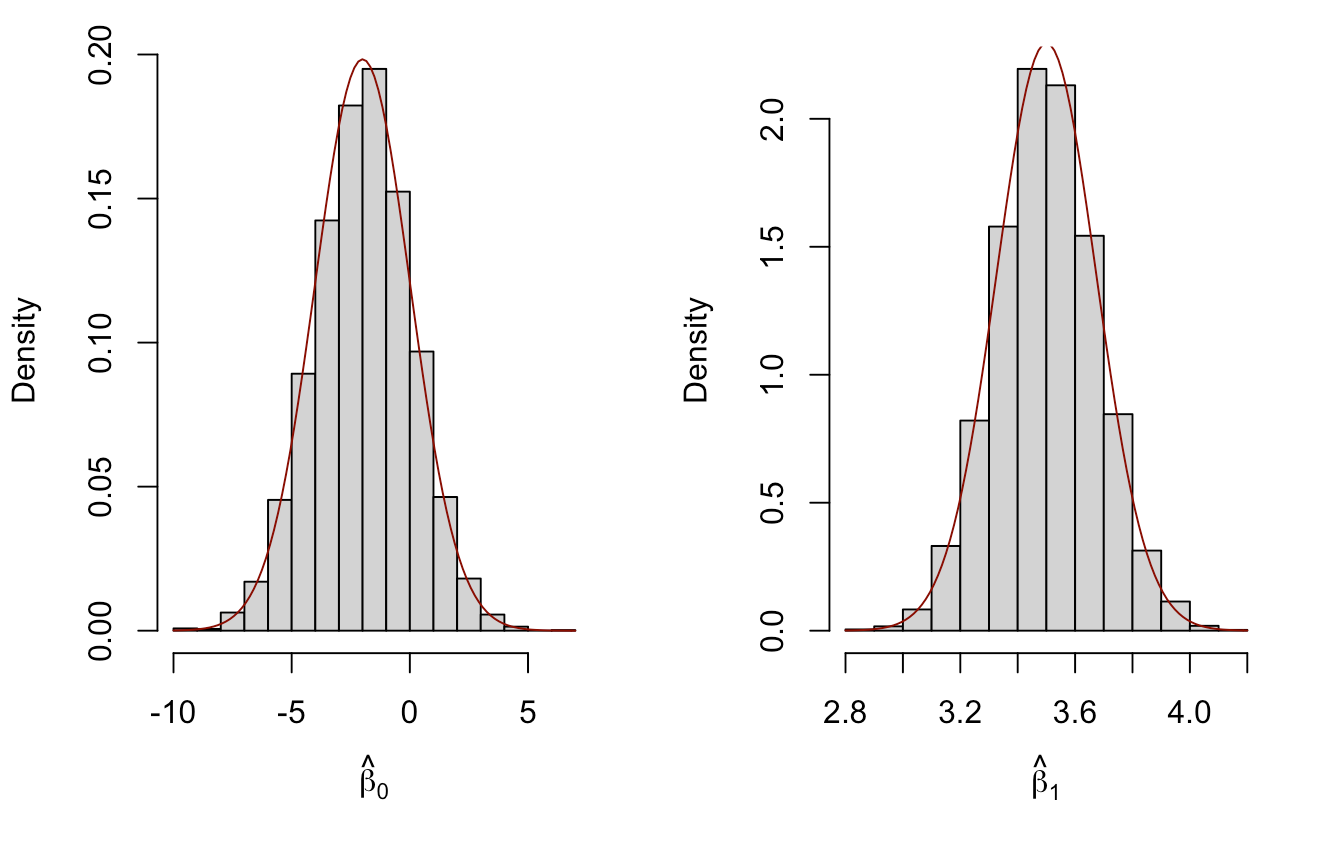
AlwaysR, Módulo III: Estadística en R
Clase 3: Modelos lineales I
Dr. Giancarlo M. Correa

Modelos lineales
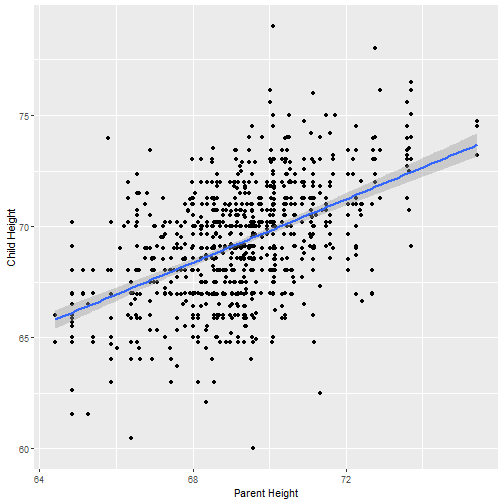
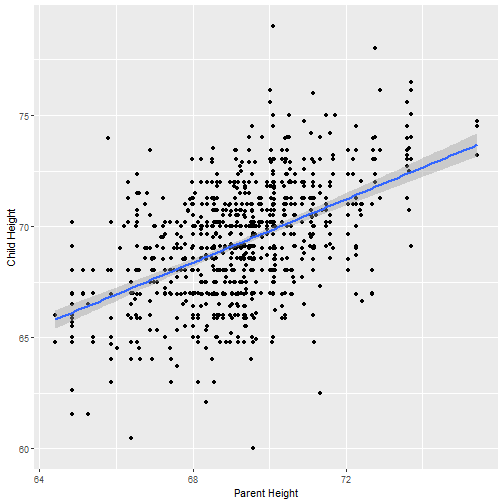
Regresión lineal simple
Establecer un modelo para:
μ(alturaniños∣alturapadres)
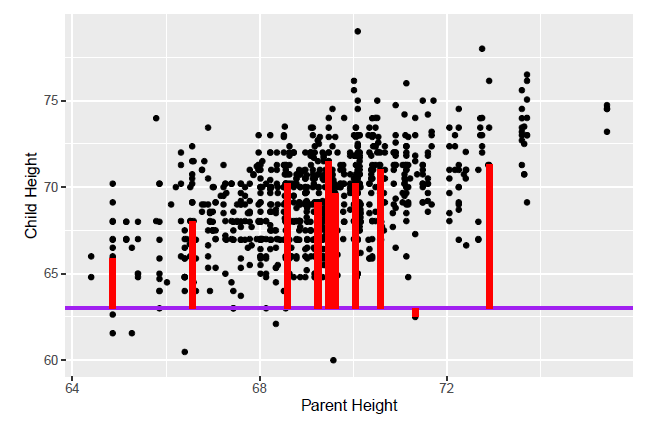
Para este caso, no estamos agrupando la altura de padres, sino estimamos una altura media de niños diferente para cada valor de la altura de padres.
Para esto usamos un modelo lineal, asumiendo que estas variables varían linealmente:
μ(alturaniños∣alturapadres)=β0+β1alturapadres
Regresión lineal simple
Establecer un modelo para:
μ(alturaniños∣alturapadres)
Para este caso, no estamos agrupando la altura de padres, sino estimamos una altura media de niños diferente para cada valor de la altura de padres.
Para esto usamos un modelo lineal, asumiendo que estas variables varían linealmente:
μ(alturaniños∣alturapadres)=β0+β1alturapadres La ecuación anterior puede ser expresada más generalmente:
μ(Y∣X)=β0+β1X
Regresión lineal simple
Establecer un modelo para:
μ(alturaniños∣alturapadres)
Para este caso, no estamos agrupando la altura de padres, sino estimamos una altura media de niños diferente para cada valor de la altura de padres.
Para esto usamos un modelo lineal, asumiendo que estas variables varían linealmente:
μ(alturaniños∣alturapadres)=β0+β1alturapadres La ecuación anterior puede ser expresada más generalmente:
μ(Y∣X)=β0+β1X
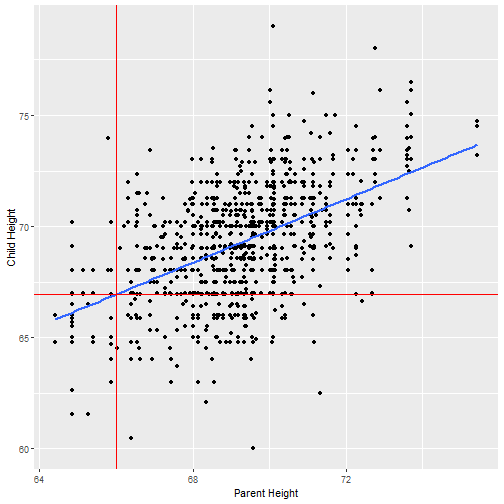
- β0: intercepto de μ(Y∣X=0)
- β1: pendiente (cuanto cambia μ(Y∣X) cuando X varía una unidad)
Regresión lineal
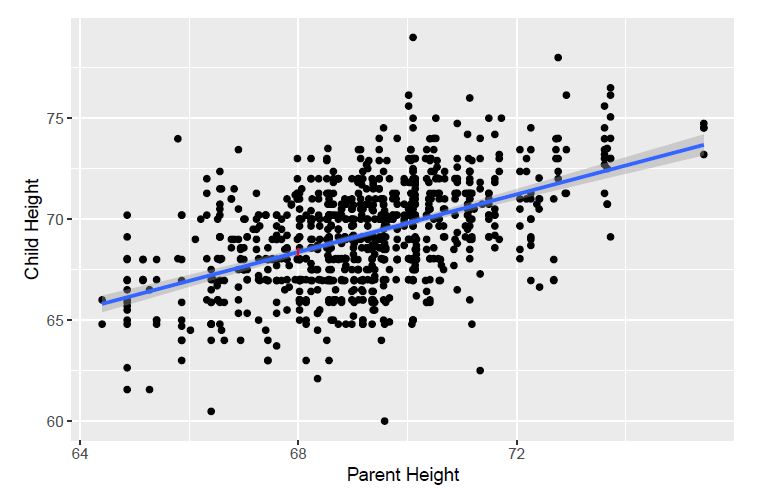
En R podemos usar (datos librería Sleuth3):
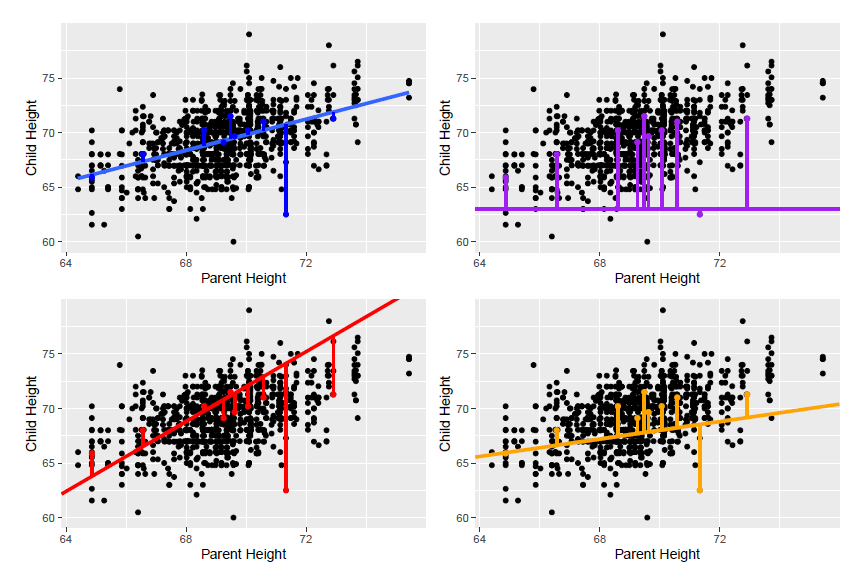
mod <- lm(cHeight ~ pHeight, data=ex0726)summary(mod)## ## Call:## lm(formula = cHeight ~ pHeight, data = ex0726)## ## Residuals:## Min 1Q Median 3Q Max ## -9.5007 -1.4864 0.0957 1.5136 9.1281 ## ## Coefficients:## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 19.82606 2.82206 7.025 4.12e-12 ***## pHeight 0.71392 0.04076 17.513 < 2e-16 ***## ---## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1## ## Residual standard error: 2.244 on 931 degrees of freedom## Multiple R-squared: 0.2478, Adjusted R-squared: 0.247 ## F-statistic: 306.7 on 1 and 931 DF, p-value: < 2.2e-16Correlación
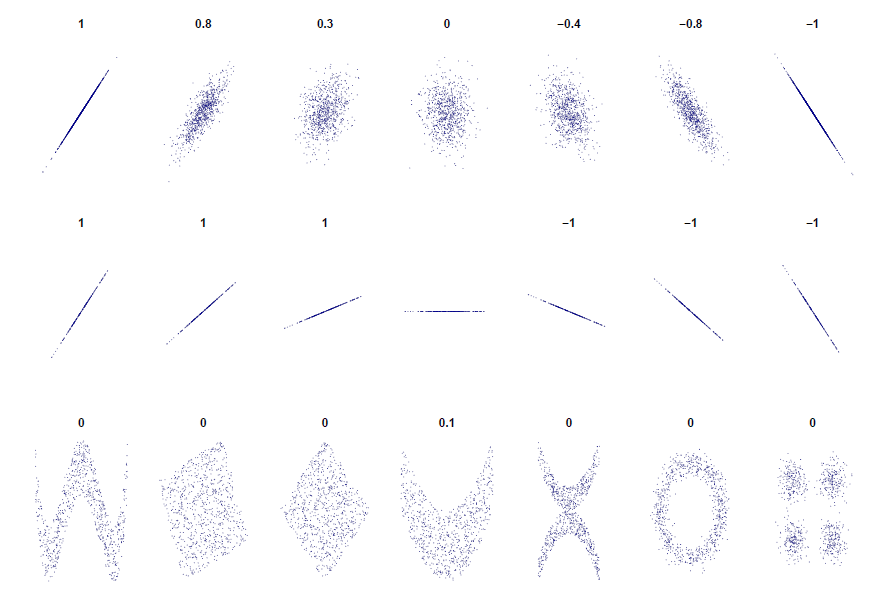
El coeficiente de correlación de la muestra rXY es una forma de medir la asociación lineal entre dos variables X e Y en una muestra de pares (Xi,Yi):
rXY=1n−1∑ni=1(Xi−¯X)(Yi−¯Y)sXsY
- rXY toma valores entre -1 y 1
- rXY=1: los puntos (Xi,Yi) caen exactamente en una línea con pendiente positiva
- rXY=−1: los puntos (Xi,Yi) caen exactamente en una línea con pendiente negativa
Correlación
El coeficiente de correlación de la muestra rXY es una forma de medir la asociación lineal entre dos variables X e Y en una muestra de pares (Xi,Yi):
rXY=1n−1∑ni=1(Xi−¯X)(Yi−¯Y)sXsY
- rXY toma valores entre -1 y 1
- rXY=1: los puntos (Xi,Yi) caen exactamente en una línea con pendiente positiva
- rXY=−1: los puntos (Xi,Yi) caen exactamente en una línea con pendiente negativa
Importante
- Correlación no nos dice la historia completa de asociación
- Correlación nos dice acerca de la fuerza de una asociación lineal
Regresión lineal
Supuestos
El modelo lineal es correcto: La media de Y es una función lineal de X. Esto es: μ(Y∣X)=β0+β1X.
Los pares de observaciones (Xi,Yi) son independientes una de otra.
La varianza de cada Yi alrededor de su media μ(Y∣X)=β0+β1X es el mismo valor σ2 (homocedasticidad).
La distribución de Yi alrededor de su media μ(Y∣X)=β0+β1X es normal.
Regresión lineal
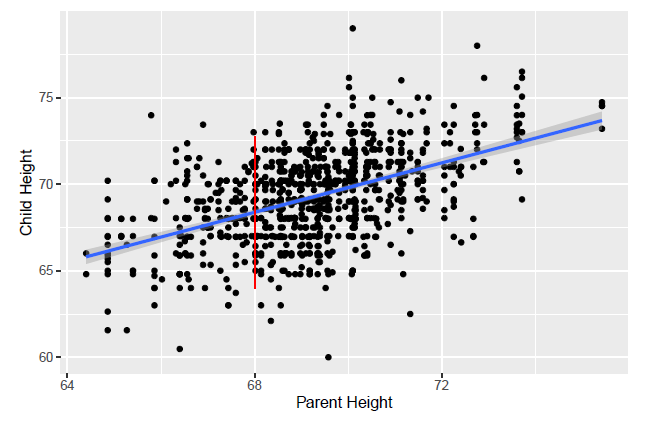
summary(mod)## ## Call:## lm(formula = cHeight ~ pHeight, data = ex0726)## ## Residuals:## Min 1Q Median 3Q Max ## -9.5007 -1.4864 0.0957 1.5136 9.1281 ## ## Coefficients:## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 19.82606 2.82206 7.025 4.12e-12 ***## pHeight 0.71392 0.04076 17.513 < 2e-16 ***## ---## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1## ## Residual standard error: 2.244 on 931 degrees of freedom## Multiple R-squared: 0.2478, Adjusted R-squared: 0.247 ## F-statistic: 306.7 on 1 and 931 DF, p-value: < 2.2e-16Inferencia
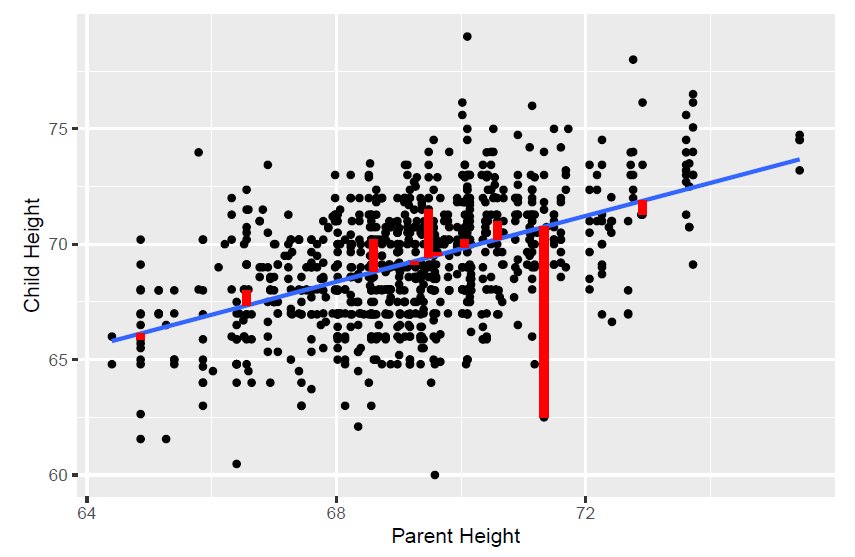
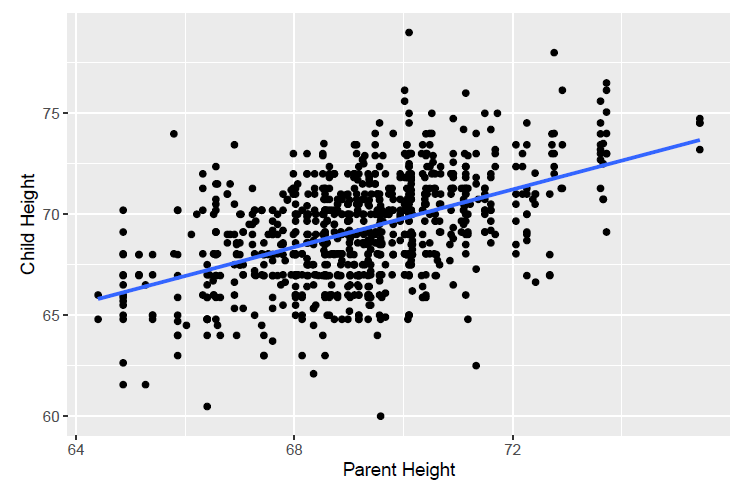
summary(mod)## ## Call:## lm(formula = cHeight ~ pHeight, data = ex0726)## ## Residuals:## Min 1Q Median 3Q Max ## -9.5007 -1.4864 0.0957 1.5136 9.1281 ## ## Coefficients:## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 19.82606 2.82206 7.025 4.12e-12 ***## pHeight 0.71392 0.04076 17.513 < 2e-16 ***## ---## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1## ## Residual standard error: 2.244 on 931 degrees of freedom## Multiple R-squared: 0.2478, Adjusted R-squared: 0.247 ## F-statistic: 306.7 on 1 and 931 DF, p-value: < 2.2e-16pi = predict(object = mod, interval = 'prediction') # intentar interval = 'confidence'newdf = cbind(ex0726, pi)ggplot(newdf, aes(x=pHeight, y=cHeight )) + geom_point() + geom_smooth(method="lm", se=TRUE) + geom_line(aes(y=lwr), color = "red", linetype = "dashed") + geom_line(aes(y=upr), color = "red", linetype = "dashed")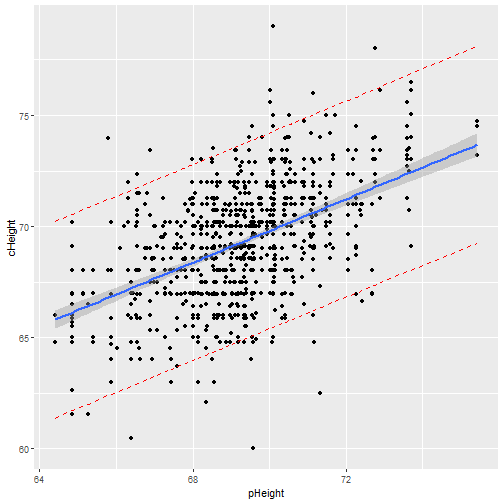
Interpretación
Pendiente
Una unidad de incremento en X está asociado con un incremento en ^β1 en la media de Y.
¿Qué significa si rechazamos H0:β1=0?
- Hay una posible tendencia lineal en la media de Y en función a X.
¿Qué significa si fallamos en rechazar H0:β1=0
- No hay evidencia (a un nivel de α, p−value=...) para una tendencia lineal en la media de Y en función a X.
Regresión múltiple
Implementar un modelo con
Una sola variable respuesta Y
2 o más variables independientes X1,X2,...,Xp
La variable respuesta debe ser continua
Las variables independientes pueden ser continuas, discretas o categóricas.
La notación es:
Yi=β0+β1Xi1+β2Xi2+...+βpXip+ϵi
Para i=1,...,n.
Interpretación
Intercepto β0: Da la respuesta media cuando todas las variables explanatorias (o independientes) son cero, esto es, cuando X1=X2=...=Xp=0.
Pendientes β1,...,βp: βj representa el cambio en la respuesta media de Y para un incremento en una unidad de la variable Xj, manteniendo todas las otras variables explanatorias constantes.
Regresión múltiple
library(yarrr)head(diamonds)## weight clarity color value## 1 9.35 0.88 4 182.5## 2 11.10 1.05 5 191.2## 3 8.65 0.85 6 175.7## 4 10.43 1.15 5 195.2## 5 10.62 0.92 5 181.6## 6 12.35 0.44 4 182.9Objetivo: Encontrar una relación entre el valor de diamante (respuesta) y otras variables explicativas (o independientes).
Unidades experimentales: 150 diamantes
Respuesta: Valor de diamante
value(dollars)Variables independientes:
weight(gramos),clarity(units),color(categórica)
Regresión múltiple
mod <- lm(formula = value ~ weight + clarity + color, data = diamonds)summary(mod)## ## Call:## lm(formula = value ~ weight + clarity + color, data = diamonds)## ## Residuals:## Min 1Q Median 3Q Max ## -10.4046 -3.5473 -0.1134 3.2552 11.0464 ## ## Coefficients:## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 148.3354 3.6253 40.917 <2e-16 ***## weight 2.1894 0.2000 10.948 <2e-16 ***## clarity 21.6922 2.1429 10.123 <2e-16 ***## color -0.4549 0.3646 -1.248 0.214 ## ---## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1## ## Residual standard error: 4.672 on 146 degrees of freedom## Multiple R-squared: 0.6373, Adjusted R-squared: 0.6298 ## F-statistic: 85.49 on 3 and 146 DF, p-value: < 2.2e-16ANOVA
Usado para comparar dos modelos anidados:
mod1 = lm(value ~ 1, data=diamonds)mod2 = lm(value ~ weight + clarity + color, data = diamonds)anova(mod1, mod2)## Analysis of Variance Table## ## Model 1: value ~ 1## Model 2: value ~ weight + clarity + color## Res.Df RSS Df Sum of Sq F Pr(>F) ## 1 149 8786.5 ## 2 146 3187.3 3 5599.2 85.495 < 2.2e-16 ***## ---## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1ANOVA
Usado para comparar dos modelos anidados:
mod1 = lm(value ~ 1, data=diamonds)mod2 = lm(value ~ weight + clarity + color, data = diamonds)anova(mod1, mod2)## Analysis of Variance Table## ## Model 1: value ~ 1## Model 2: value ~ weight + clarity + color## Res.Df RSS Df Sum of Sq F Pr(>F) ## 1 149 8786.5 ## 2 146 3187.3 3 5599.2 85.495 < 2.2e-16 ***## ---## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1- H0: β1=β2=β3=0
- HA: al menos uno de β1 o β2 o β3 no es cero.
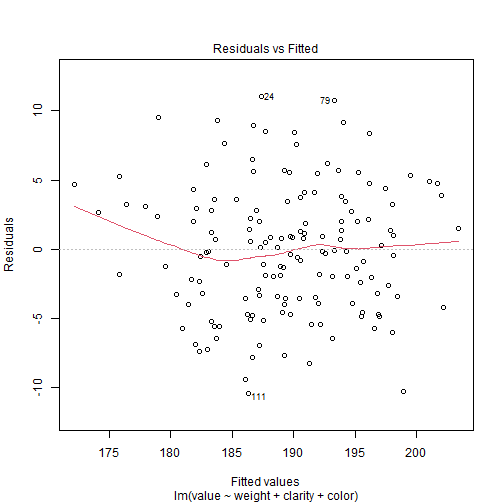
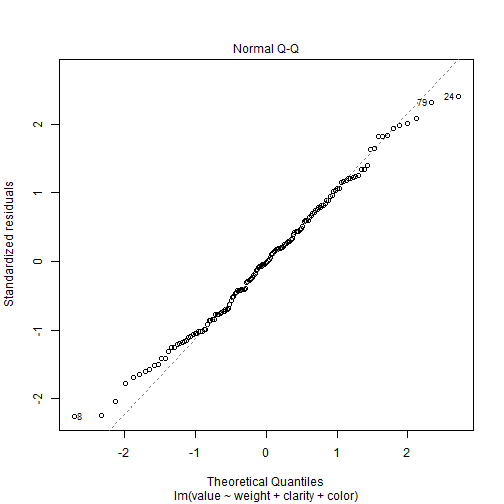
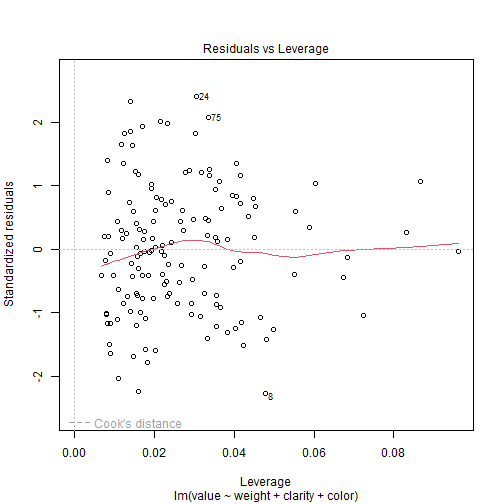
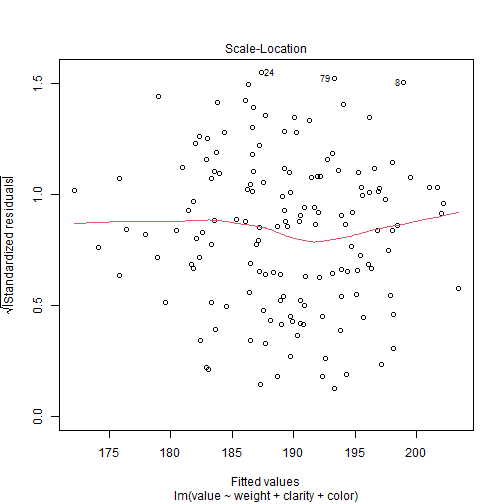
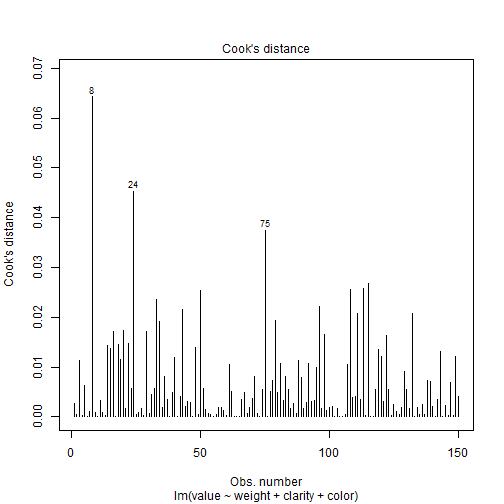
Revisión del modelo
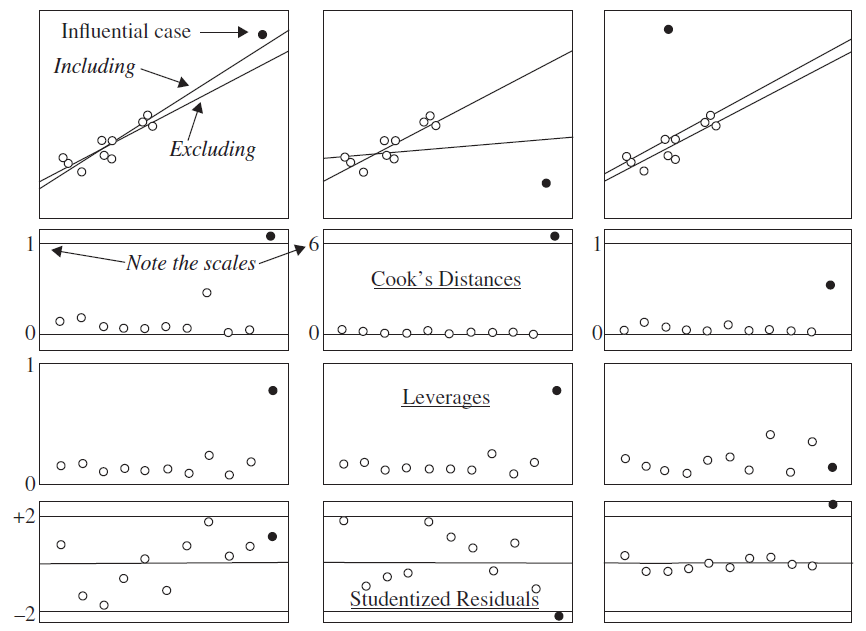
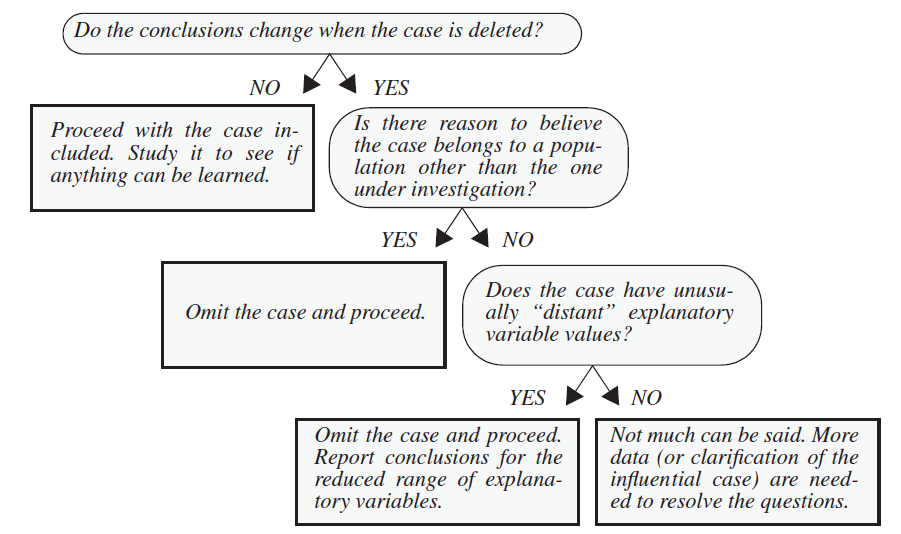
Existen tres tipos de observaciones raras que podemos mencionar:
Una observación es dicha tener un alto leverage si el valor de la observación de la variable explanatoria es diferente del patrón general (solo en el espacio de las variables explanatorias).
Una observación es un outlier si la observación no se ajusta dentro del modelo ajustado.
Una observación es dicha ser influyente si el modelo ajustado depende indudablemente de su valor (i.e. cuando esta observación se remueve, los parámetros estimados cambian enormemente).
Regresión múltiple: interacción
Tenemos el modelo:
E(Y∣X1,X2)=β0+β1X1+β2X2
En este caso X1 es continua y X2 es una categórica de dos niveles (0 y 1).
Podemos incorporar una interacción:
E(Y∣X1,X2)=β0+β1X1+β2X2+β3(X1X2)
Dos variables interactúan si el efecto de una variable sobre la respuesta media depende de la otra variable.
Regresión múltiple: interacción
Tenemos el modelo:
E(Y∣X1,X2)=β0+β1X1+β2X2
En este caso X1 es continua y X2 es una categórica de dos niveles (0 y 1).
Podemos incorporar una interacción:
E(Y∣X1,X2)=β0+β1X1+β2X2+β3(X1X2)
Dos variables interactúan si el efecto de una variable sobre la respuesta media depende de la otra variable.
β3(X1X2) es llamado el término de interacción. Permite que el efecto de X1 sobre la media de Y dependa en X2=0 o X2=1.
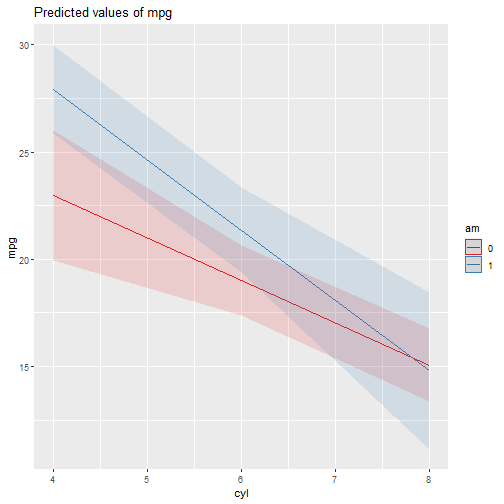
mod1 = lm(mpg ~ cyl + am + cyl * am, data = mtcars)summary(mod1)## ## Call:## lm(formula = mpg ~ cyl + am + cyl * am, data = mtcars)## ## Residuals:## Min 1Q Median 3Q Max ## -6.5255 -1.2820 -0.0191 1.6301 5.9745 ## ## Coefficients:## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 30.8735 3.1882 9.684 1.95e-10 ***## cyl -1.9757 0.4485 -4.405 0.000141 ***## am1 10.1754 4.3046 2.364 0.025258 * ## cyl:am1 -1.3051 0.7070 -1.846 0.075507 . ## ---## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1## ## Residual standard error: 2.939 on 28 degrees of freedom## Multiple R-squared: 0.7852, Adjusted R-squared: 0.7621 ## F-statistic: 34.11 on 3 and 28 DF, p-value: 1.73e-09Regresión múltiple: interacción
Basado en el ejemplo anterior, el modelo es:
E(Y∣X1,X2)=β0+β1X1+β2X2+β3(X1X2)
Interpretación:
β0: es la media de Y cuando X1 y X2 son iguales a cero (intercepto).
β1: da el cambio en la media de Y cuando X1 es incrementado por una unidad y X2=0.
β2: da el cambio en la media de Y cuando X2 cambia de 0 a 1 y X1 es mantenido en cero.
Regresión múltiple: interacción
Basado en el ejemplo anterior, el modelo es:
E(Y∣X1,X2)=β0+β1X1+β2X2+β3(X1X2)
Interpretación:
β0: es la media de Y cuando X1 y X2 son iguales a cero (intercepto).
β1: da el cambio en la media de Y cuando X1 es incrementado por una unidad y X2=0.
β2: da el cambio en la media de Y cuando X2 cambia de 0 a 1 y X1 es mantenido en cero.
β3: da la diferencia en el cambio en la media de Y cuando X1 es incrementado en una unidad cuando X2=1, comparado al cambio en la media de Y cuando X1 es incrementado en una unidad cuando X2=0.