AlwaysR, Módulo III: Estadística en R

Clase 4: Modelos lineales II. Efectos aleatorios.

Dr. Giancarlo M. Correa

1 / 42

Modelos lineales II

2 / 42

Librerías a utilizar

A lo largo de esta clase, utilizaremos:

library(sjPlot)
library(ggeffects)
library(sjmisc)
library(ggplot2)
library(faraway)
library(Sleuth3)
library(nlme)
library(effects)
library(olsrr)
library(glmmTMB)
library(lme4)

3 / 42

Problemas con datos

Multicolinealidad

No genera problemas estadísticos, sin embargo, genera problemas en la interpretación.

4 / 42

Problemas con datos

Multicolinealidad

No genera problemas estadísticos, sin embargo, genera problemas en la interpretación.
No tiene sentido interpretar el efecto de $X_{1}$ manteniendo otras variables independientes constante porque nosotros hemos observado una relación entre $X_{1}$ y otras variables.

4 / 42

Problemas con datos

Multicolinealidad

No genera problemas estadísticos, sin embargo, genera problemas en la interpretación.
No tiene sentido interpretar el efecto de $X_{1}$ manteniendo otras variables independientes constante porque nosotros hemos observado una relación entre $X_{1}$ y otras variables.

head(seatpos)

##   Age Weight HtShoes    Ht Seated  Arm Thigh  Leg hipcenter
## 1  46    180   187.2 184.9   95.2 36.1  45.3 41.3  -206.300
## 2  31    175   167.5 165.5   83.8 32.9  36.5 35.9  -178.210
## 3  23    100   153.6 152.2   82.9 26.0  36.6 31.0   -71.673
## 4  19    185   190.3 187.4   97.3 37.4  44.1 41.0  -257.720
## 5  23    159   178.0 174.1   93.9 29.5  40.1 36.9  -173.230
## 6  47    170   178.7 177.0   92.4 36.0  43.2 37.4  -185.150

4 / 42

mod2 = lm(hipcenter ~ ., data = seatpos)
summary(mod2)

## 
## Call:
## lm(formula = hipcenter ~ ., data = seatpos)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -73.827 -22.833  -3.678  25.017  62.337 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)  
## (Intercept) 436.43213  166.57162   2.620   0.0138 *
## Age           0.77572    0.57033   1.360   0.1843  
## Weight        0.02631    0.33097   0.080   0.9372  
## HtShoes      -2.69241    9.75304  -0.276   0.7845  
## Ht            0.60134   10.12987   0.059   0.9531  
## Seated        0.53375    3.76189   0.142   0.8882  
## Arm          -1.32807    3.90020  -0.341   0.7359  
## Thigh        -1.14312    2.66002  -0.430   0.6706  
## Leg          -6.43905    4.71386  -1.366   0.1824  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 37.72 on 29 degrees of freedom
## Multiple R-squared:  0.6866,    Adjusted R-squared:  0.6001 
## F-statistic:  7.94 on 8 and 29 DF,  p-value: 1.306e-05

5 / 42

Problemas con datos

La matriz de correlación entre todas las variables:

round(cor(seatpos), digits = 2)

##             Age Weight HtShoes    Ht Seated   Arm Thigh   Leg hipcenter
## Age        1.00   0.08   -0.08 -0.09  -0.17  0.36  0.09 -0.04      0.21
## Weight     0.08   1.00    0.83  0.83   0.78  0.70  0.57  0.78     -0.64
## HtShoes   -0.08   0.83    1.00  1.00   0.93  0.75  0.72  0.91     -0.80
## Ht        -0.09   0.83    1.00  1.00   0.93  0.75  0.73  0.91     -0.80
## Seated    -0.17   0.78    0.93  0.93   1.00  0.63  0.61  0.81     -0.73
## Arm        0.36   0.70    0.75  0.75   0.63  1.00  0.67  0.75     -0.59
## Thigh      0.09   0.57    0.72  0.73   0.61  0.67  1.00  0.65     -0.59
## Leg       -0.04   0.78    0.91  0.91   0.81  0.75  0.65  1.00     -0.79
## hipcenter  0.21  -0.64   -0.80 -0.80  -0.73 -0.59 -0.59 -0.79      1.00

6 / 42

Problemas con datos

¿Qué podemos hacer cuando tenemos variables correlacionadas?

Seleccionar las variables más importantes

7 / 42

Problemas con datos

¿Qué podemos hacer cuando tenemos variables correlacionadas?

Seleccionar las variables más importantes
Identificar las variables correlacionadas claves para el modelo: variance inflation factors (VIF)

7 / 42

Problemas con datos

¿Qué podemos hacer cuando tenemos variables correlacionadas?

Seleccionar las variables más importantes
Identificar las variables correlacionadas claves para el modelo: variance inflation factors (VIF)

round(vif(mod2), digits = 2)

##     Age  Weight HtShoes      Ht  Seated     Arm   Thigh     Leg 
##    2.00    3.65  307.43  333.14    8.95    4.50    2.76    6.69

Valores $V I F_{j} > 10$ indican una alta colinealidad.

7 / 42

Problemas con datos

¿Qué podemos hacer cuando tenemos variables correlacionadas?

Seleccionar las variables más importantes
Identificar las variables correlacionadas claves para el modelo: variance inflation factors (VIF)

round(vif(mod2), digits = 2)

##     Age  Weight HtShoes      Ht  Seated     Arm   Thigh     Leg 
##    2.00    3.65  307.43  333.14    8.95    4.50    2.76    6.69

Valores $V I F_{j} > 10$ indican una alta colinealidad.

Eliminar algunas variables no significa que ellas no están asociadas con la variable respuesta, solo que no las necesitamos para predecir la respuesta.

7 / 42

Datos faltantes

Podemos hablar de dos casos:

Caso faltante: cuando no tenemos información de todas las variables en una observación en el conjunto de datos.

8 / 42

Datos faltantes

Podemos hablar de dos casos:

Caso faltante: cuando no tenemos información de todas las variables en una observación en el conjunto de datos.
Valores faltantes: cuando no tenemos información de algunas variables en una observación en el conjunto de datos.

8 / 42

Datos faltantes

Podemos hablar de dos casos:

Caso faltante: cuando no tenemos información de todas las variables en una observación en el conjunto de datos.
Valores faltantes: cuando no tenemos información de algunas variables en una observación en el conjunto de datos.

head(chmiss, n = 10)

##       race fire theft  age involact income
## 60626 10.0  6.2    29 60.4       NA 11.744
## 60640 22.2  9.5    44 76.5      0.1  9.323
## 60613 19.6 10.5    36   NA      1.2  9.948
## 60657 17.3  7.7    37   NA      0.5 10.656
## 60614 24.5  8.6    53 81.4      0.7  9.730
## 60610 54.0 34.1    68 52.6      0.3  8.231
## 60611  4.9 11.0    75 42.6      0.0 21.480
## 60625  7.1  6.9    18 78.5      0.0 11.104
## 60618  5.3  7.3    31 90.1       NA 10.694
## 60647 21.5 15.1    NA 89.8      1.1  9.631

8 / 42

Datos faltantes

Hay dos enfoques para lidiar con esto:

Métodos de supresión: eliminar las observaciones con algun tipo de datos faltantes.

9 / 42

Datos faltantes

Hay dos enfoques para lidiar con esto:

Métodos de supresión: eliminar las observaciones con algun tipo de datos faltantes.
Métodos de retención: retienen las observaciones con datos faltantes para implementar una regresión modificada para datos faltantes.

9 / 42

Datos faltantes

Hay dos enfoques para lidiar con esto:

Métodos de supresión: eliminar las observaciones con algun tipo de datos faltantes.
Métodos de retención: retienen las observaciones con datos faltantes para implementar una regresión modificada para datos faltantes.

Método de supresión

Simplemente eliminar las observaciones con datos faltantes e implementar el modelo luego. R hace esto por nosotros automaticamente.

##       race fire theft  age involact income
## 60626 10.0  6.2    29 60.4       NA 11.744
## 60640 22.2  9.5    44 76.5      0.1  9.323
## 60613 19.6 10.5    36   NA      1.2  9.948
## 60657 17.3  7.7    37   NA      0.5 10.656
## 60614 24.5  8.6    53 81.4      0.7  9.730
## 60610 54.0 34.1    68 52.6      0.3  8.231
## 60611  4.9 11.0    75 42.6      0.0 21.480

9 / 42

Método de retención

Imputación: completar los datos perdidos con la media de cada variable. Se puede usar también la mediana, moda, etc. Problemas: Introduce error. Métodos de estimación de parámetros pueden estar sesgados.

10 / 42

Método de retención

Imputación: completar los datos perdidos con la media de cada variable. Se puede usar también la mediana, moda, etc. Problemas: Introduce error. Métodos de estimación de parámetros pueden estar sesgados.
Imputación a partir de regresión: Implementar un modelo lineal con las observaciones completas. Luego, predecir valores cuando hayan datos faltantes. En este caso, la variable respuesta será la variable que tiene datos faltantes y las variables independientes todas las demás variables.

10 / 42

Selección de modelos

El proceso de seleccionar tan pocas variables como sea posible para incluir en el modelo lineal (principio de parsimonia).

11 / 42

Selección de modelos

El proceso de seleccionar tan pocas variables como sea posible para incluir en el modelo lineal (principio de parsimonia).

head(case1201)

##         State  SAT Takers Income Years Public Expend Rank
## 1        Iowa 1088      3    326 16.79   87.8  25.60 89.7
## 2 SouthDakota 1075      2    264 16.07   86.2  19.95 90.6
## 3 NorthDakota 1068      3    317 16.57   88.3  20.62 89.8
## 4      Kansas 1045      5    338 16.30   83.9  27.14 86.3
## 5    Nebraska 1045      5    293 17.25   83.6  21.05 88.5
## 6     Montana 1033      8    263 15.91   93.7  29.48 86.4

11 / 42

mod3 = lm(SAT ~ Takers + Income + Years + Public + Expend + Rank, data=case1201)
summary(mod3)

## 
## Call:
## lm(formula = SAT ~ Takers + Income + Years + Public + Expend + 
##     Rank, data = case1201)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -60.046  -6.768   0.972  13.947  46.332 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -94.659109 211.509584  -0.448 0.656731    
## Takers       -0.480080   0.693711  -0.692 0.492628    
## Income       -0.008195   0.152358  -0.054 0.957353    
## Years        22.610082   6.314577   3.581 0.000866 ***
## Public       -0.464152   0.579104  -0.802 0.427249    
## Expend        2.212005   0.845972   2.615 0.012263 *  
## Rank          8.476217   2.107807   4.021 0.000230 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 26.34 on 43 degrees of freedom
## Multiple R-squared:  0.8787,    Adjusted R-squared:  0.8618 
## F-statistic: 51.91 on 6 and 43 DF,  p-value: < 2.2e-16

12 / 42

Selección de modelos

Con esta base de datos, el modelo más simple que podemos implementar es:

$S A T_{i} = β_{0} + ϵ_{i}$

13 / 42

Selección de modelos

Con esta base de datos, el modelo más simple que podemos implementar es:

$S A T_{i} = β_{0} + ϵ_{i}$

El modelo más complicado es:

$S A T_{i} = β_{0} + β_{1} I n c o m e_{i} + β_{2} T a k e r s_{i} + β_{3} Y e a r s_{i} + β_{4} R a n k_{i} + β_{5} E x p e n d_{i} + β_{6} P u b l i c_{i} + ϵ_{i}$

13 / 42

Selección de modelos

Con esta base de datos, el modelo más simple que podemos implementar es:

$S A T_{i} = β_{0} + ϵ_{i}$

El modelo más complicado es:

$S A T_{i} = β_{0} + β_{1} I n c o m e_{i} + β_{2} T a k e r s_{i} + β_{3} Y e a r s_{i} + β_{4} R a n k_{i} + β_{5} E x p e n d_{i} + β_{6} P u b l i c_{i} + ϵ_{i}$

¿Cuantos modelos podemos implementar con esta base de datos?

13 / 42

Selección de modelos

Con esta base de datos, el modelo más simple que podemos implementar es:

$S A T_{i} = β_{0} + ϵ_{i}$

El modelo más complicado es:

$S A T_{i} = β_{0} + β_{1} I n c o m e_{i} + β_{2} T a k e r s_{i} + β_{3} Y e a r s_{i} + β_{4} R a n k_{i} + β_{5} E x p e n d_{i} + β_{6} P u b l i c_{i} + ϵ_{i}$

¿Cuantos modelos podemos implementar con esta base de datos?

$2^{6}$ modelos posibles! (sin considerar interacciones!)

13 / 42

Selección de modelos

Eliminación hacia atrás: Comienza con el full model. Elimina la variable con mayor p-value y corre el modelo nuevamente. Repite este proceso hasta que el modelo solo contiene variables con p-value por dejabo de nivel de significancia $α$ .

14 / 42

Selección de modelos

Eliminación hacia atrás: Comienza con el full model. Elimina la variable con mayor p-value y corre el modelo nuevamente. Repite este proceso hasta que el modelo solo contiene variables con p-value por dejabo de nivel de significancia $α$ .
Selección hacia adelante: Comienza con el modelo más sencillo (solo contiene intercepto). Añade la variable con menor p-value por debajo de nivel de significancia $α$ . Repetir hasta que no haya variable que pueda ser añadida con p-value por debajo de nivel de significancia $α$ .

14 / 42

Selección de modelos

Eliminación hacia atrás: Comienza con el full model. Elimina la variable con mayor p-value y corre el modelo nuevamente. Repite este proceso hasta que el modelo solo contiene variables con p-value por dejabo de nivel de significancia $α$ .
Selección hacia adelante: Comienza con el modelo más sencillo (solo contiene intercepto). Añade la variable con menor p-value por debajo de nivel de significancia $α$ . Repetir hasta que no haya variable que pueda ser añadida con p-value por debajo de nivel de significancia $α$ .

Limitaciones

Inclusión en el modelo no necesariamente significa que la variable es importante.
Exclusión no necesariamente significa que la variable no sea importante.
Se tiende a elegir los modelos más pequeños que los óptimos para predicción.

14 / 42

mod3 = lm(SAT ~ Takers + Income + Years + Public + Expend + Rank, data=case1201)
backmod = ols_step_backward_p(mod3, prem=0.05, progress=FALSE) # Seleccion hacia atras
summary(backmod$model)

## 
## Call:
## lm(formula = paste(response, "~", paste(preds, collapse = " + ")), 
##     data = l)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -64.802  -6.798   2.169  17.525  49.706 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -303.7243    97.8415  -3.104  0.00326 ** 
## Years         26.0952     5.3894   4.842 1.49e-05 ***
## Expend         1.8609     0.6351   2.930  0.00526 ** 
## Rank           9.8258     0.5987  16.412  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 26.25 on 46 degrees of freedom
## Multiple R-squared:  0.8711,    Adjusted R-squared:  0.8627 
## F-statistic: 103.6 on 3 and 46 DF,  p-value: < 2.2e-16

15 / 42

mod3 = lm(SAT ~ Takers + Income + Years + Public + Expend + Rank, data=case1201)
forwardmod = ols_step_forward_p(mod3, penter=0.05, progress=FALSE) # Seleccion hacia adelante
summary(forwardmod$model)

## 
## Call:
## lm(formula = paste(response, "~", paste(preds, collapse = " + ")), 
##     data = l)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -64.802  -6.798   2.169  17.525  49.706 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -303.7243    97.8415  -3.104  0.00326 ** 
## Rank           9.8258     0.5987  16.412  < 2e-16 ***
## Years         26.0952     5.3894   4.842 1.49e-05 ***
## Expend         1.8609     0.6351   2.930  0.00526 ** 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 26.25 on 46 degrees of freedom
## Multiple R-squared:  0.8711,    Adjusted R-squared:  0.8627 
## F-statistic: 103.6 on 3 and 46 DF,  p-value: < 2.2e-16

16 / 42

Selección de modelos

Métodos basados en criterio:

$A I C$ : Criterio de información de Akaike. Toma en cuenta el número de observaciones, parámetros, y suma de residuales. Normalmente el menor $A I C$ nos indica un mejor modelo.
$B I C$ : Criterio de información Bayesiana. Toma en cuenta el número de observaciones, parámetros, y suma de residuales. Normalmente el menor $B I C$ nos indica un mejor modelo.
$R^{2} - a d j$ : El mayor valor nos indica el mejor modelo.

17 / 42

Selección de modelos

Métodos basados en criterio:

$A I C$ : Criterio de información de Akaike. Toma en cuenta el número de observaciones, parámetros, y suma de residuales. Normalmente el menor $A I C$ nos indica un mejor modelo.
$B I C$ : Criterio de información Bayesiana. Toma en cuenta el número de observaciones, parámetros, y suma de residuales. Normalmente el menor $B I C$ nos indica un mejor modelo.
$R^{2} - a d j$ : El mayor valor nos indica el mejor modelo.

Si deseas obtener el mejor modelo, se recomienda usar $B I C$ .

Si deseas usar el modelo para hacer predicciones, se recomienda usar $A I C$ .

Los modelos no necesitan ser anidados para ser comparados (pero si deben contener los mismos datos).

17 / 42

mod4 = lm(SAT ~ Years + Expend + Rank, data=case1201)
summ4 = summary(mod4)
mod5 = lm(SAT ~ Income + Years + Expend + Rank, data=case1201)
summ5 = summary(mod5)

Comparar modelos con $R^{2} - a d j$ :

summ4$adj.r.squared

## [1] 0.8627047

summ5$adj.r.squared

## [1] 0.8634092

18 / 42

Comparar modelos con $A I C$ :

AIC(mod4)

## [1] 474.5092

AIC(mod5)

## [1] 475.1531

19 / 42

Comparar modelos con $A I C$ :

AIC(mod4)

## [1] 474.5092

AIC(mod5)

## [1] 475.1531

Comparar modelos con $B I C$ :

BIC(mod4)

## [1] 484.0694

BIC(mod5)

## [1] 486.6252

19 / 42

Problemas con supuestos

20 / 42

Problemas con supuestos

Linealidad de la asociación

Consecuencia depende en el grado de no-linealidad.
Buscar alternativas (e.g. modelos aditivos generalizados, splines, etc.)

20 / 42

Problemas con supuestos

Linealidad de la asociación

Consecuencia depende en el grado de no-linealidad.
Buscar alternativas (e.g. modelos aditivos generalizados, splines, etc.)

Independencia

Un modelo lineal no es robusto a la no independencia de observaciones.
Alternativa, usar la función gls en caso de dependencia temporal (siempre y cuando se conozca la estructura del error).

20 / 42

Problemas con supuestos

Linealidad de la asociación

Consecuencia depende en el grado de no-linealidad.
Buscar alternativas (e.g. modelos aditivos generalizados, splines, etc.)

Independencia

Un modelo lineal no es robusto a la no independencia de observaciones.
Alternativa, usar la función gls en caso de dependencia temporal (siempre y cuando se conozca la estructura del error).

Normalidad

Si se tiene un muestreo grande $n$ , este supuesto no causa problemas importantes.
Se recomienda usar ejercicios de simulación para saber los efectos de la no-normalidad de residuos sobre los parámetros estimados.

20 / 42

Transformaciones

Pueden ayudar en el ajuste del modelo y cumplir los supuestos de la regresión lineal (e.g. supuesto de varianza constante).

21 / 42

Transformaciones

Pueden ayudar en el ajuste del modelo y cumplir los supuestos de la regresión lineal (e.g. supuesto de varianza constante).

En vez de $Y_{i} = β_{0} + β_{1} X_{i} + ϵ_{i}$ , podemos escribir:

$l o g (Y_{i}) = β_{0} + β_{1} X_{i} + ϵ_{i}$

21 / 42

Transformaciones

Pueden ayudar en el ajuste del modelo y cumplir los supuestos de la regresión lineal (e.g. supuesto de varianza constante).

En vez de $Y_{i} = β_{0} + β_{1} X_{i} + ϵ_{i}$ , podemos escribir:

$l o g (Y_{i}) = β_{0} + β_{1} X_{i} + ϵ_{i}$

Despues de ajustar el modelo, tenemos que volver a la escala original:

$Y_{i} = e x p (β_{0} + β_{1} X_{i}) e x p (ϵ_{i})$

21 / 42

Transformaciones

Pueden ayudar en el ajuste del modelo y cumplir los supuestos de la regresión lineal (e.g. supuesto de varianza constante).

En vez de $Y_{i} = β_{0} + β_{1} X_{i} + ϵ_{i}$ , podemos escribir:

$l o g (Y_{i}) = β_{0} + β_{1} X_{i} + ϵ_{i}$

Despues de ajustar el modelo, tenemos que volver a la escala original:

$Y_{i} = e x p (β_{0} + β_{1} X_{i}) e x p (ϵ_{i})$

Obtener la variable respuesta en su escala original no es muy complicado. Sin embargo, los coeficientes estimados ya no tienen la misma interpretación. Por ejemplo:

Un incremento en una unidad en $X_{1}$ ahora multiplicaría la respuesta media (en su escala original) por $e^{\hat{β_{1}}}$ .

21 / 42

Transformaciones

Pueden ayudar en el ajuste del modelo y cumplir los supuestos de la regresión lineal (e.g. supuesto de varianza constante).

En vez de $Y_{i} = β_{0} + β_{1} X_{i} + ϵ_{i}$ , podemos escribir:

$l o g (Y_{i}) = β_{0} + β_{1} X_{i} + ϵ_{i}$

Despues de ajustar el modelo, tenemos que volver a la escala original:

$Y_{i} = e x p (β_{0} + β_{1} X_{i}) e x p (ϵ_{i})$

Obtener la variable respuesta en su escala original no es muy complicado. Sin embargo, los coeficientes estimados ya no tienen la misma interpretación. Por ejemplo:

Un incremento en una unidad en $X_{1}$ ahora multiplicaría la respuesta media (en su escala original) por $e^{\hat{β_{1}}}$ .

Para mayor información sobre transformaciones, ver aquí.

21 / 42

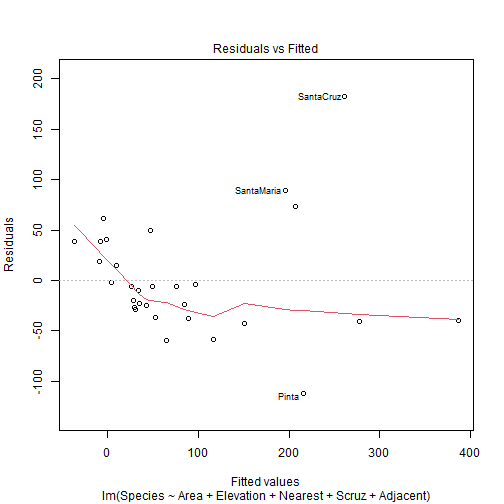
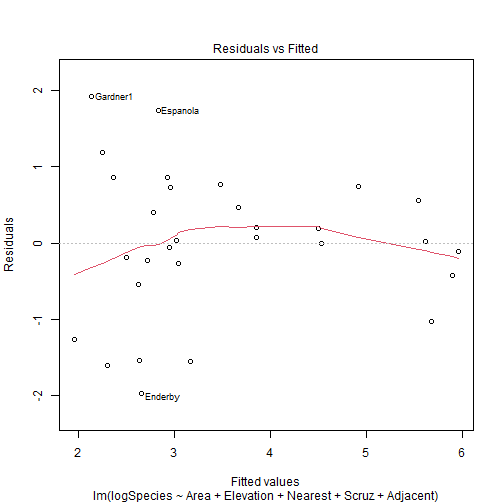
head(gala)

##              Species Endemics  Area Elevation Nearest Scruz Adjacent
## Baltra            58       23 25.09       346     0.6   0.6     1.84
## Bartolome         31       21  1.24       109     0.6  26.3   572.33
## Caldwell           3        3  0.21       114     2.8  58.7     0.78
## Champion          25        9  0.10        46     1.9  47.4     0.18
## Coamano            2        1  0.05        77     1.9   1.9   903.82
## Daphne.Major      18       11  0.34       119     8.0   8.0     1.84

22 / 42

lmod = lm(Species ~ Area + Elevation + Nearest + Scruz + Adjacent, data=gala)
plot(lmod, which=1)

23 / 42

gala$logSpecies = log(gala$Species)
lmod = lm(logSpecies ~ Area + Elevation + Nearest + Scruz + Adjacent, data=gala)
plot(lmod, which=1)

24 / 42

Efectos aleatorios25 / 42

Efectos aleatorios

Modelo de efectos mixtos: cuando tenemos efectos fijos (como hemos visto hasta el momento) y efectos aleatorios (como describiremos aquí).

26 / 42

Efectos aleatorios

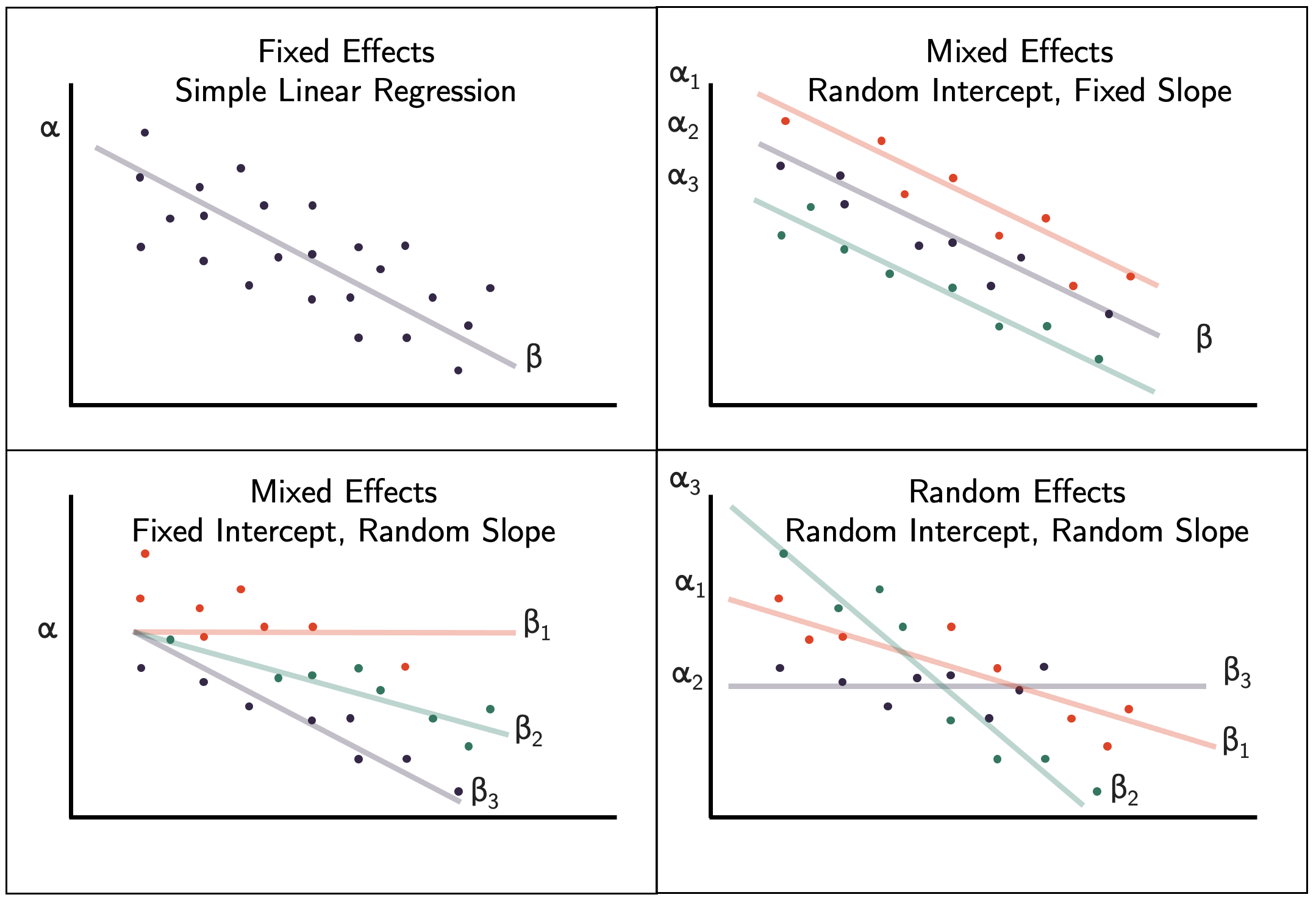
Modelo de efectos mixtos: cuando tenemos efectos fijos (como hemos visto hasta el momento) y efectos aleatorios (como describiremos aquí).
Efecto fijo: Son variables que esperamos tengan un efecto sobre la variable respuesta ( $Y$ ). Es decir, es el $X$ como lo hemos visto hasta el momento. Puede ser continua o categórica. Se asume que no hay relación entre los diferentes niveles de una variable. Ejemplo: un efecto para hembras y un efecto para machos, pero estos efectos no interactúan uno con el otro.

26 / 42

Efectos aleatorios

Modelo de efectos mixtos: cuando tenemos efectos fijos (como hemos visto hasta el momento) y efectos aleatorios (como describiremos aquí).
Efecto fijo: Son variables que esperamos tengan un efecto sobre la variable respuesta ( $Y$ ). Es decir, es el $X$ como lo hemos visto hasta el momento. Puede ser continua o categórica. Se asume que no hay relación entre los diferentes niveles de una variable. Ejemplo: un efecto para hembras y un efecto para machos, pero estos efectos no interactúan uno con el otro.
Efecto aleatorio: Son factores de agrupación que tratamos de controlar. Siempre son variables categóricas. Normalmente no estamos interesados en el efecto de esta variable sobre nuestra variable respuesta $Y$ , pero sabemos que puede influir en nuestros resultados. Los niveles o grupos en un efecto aleatorio puede ser pensado como una muestra de niveles de una población más grande de niveles. Se recomienda un mínimo de 5 niveles en nuestros datos.

26 / 42

Efectos aleatorios

27 / 42

Efectos aleatorios

Tomar en cuenta:

No usar efectos aleatorios cuando el número de niveles es bajo (3 o menor).
No usar efectos aleatorios cuando no se quiere asumir que estos niveles vienen de una distribución común en la población.

28 / 42

Efectos aleatorios

Tomar en cuenta:

No usar efectos aleatorios cuando el número de niveles es bajo (3 o menor).
No usar efectos aleatorios cuando no se quiere asumir que estos niveles vienen de una distribución común en la población.

¿En qué casos debo incorporar efectos aleatorios?

¿Los factores pueden ser considerados como una muestra aleatoria de una distribución de probabilidad?
¿La investigación tiene por objetivo hacer inferencia a una población mayor a la incluida en el modelo?
¿Hay una falta de independencia estadística debido a múltiples observaciones para un mismo nivel?

28 / 42

Efectos aleatorios

head(sleepstudy, n = 25)

##    Reaction Days Subject
## 1  249.5600    0     308
## 2  258.7047    1     308
## 3  250.8006    2     308
## 4  321.4398    3     308
## 5  356.8519    4     308
## 6  414.6901    5     308
## 7  382.2038    6     308
## 8  290.1486    7     308
## 9  430.5853    8     308
## 10 466.3535    9     308
## 11 222.7339    0     309
## 12 205.2658    1     309
## 13 202.9778    2     309
## 14 204.7070    3     309
## 15 207.7161    4     309
## 16 215.9618    5     309
## 17 213.6303    6     309
## 18 217.7272    7     309
## 19 224.2957    8     309
## 20 237.3142    9     309
## 21 199.0539    0     310
## 22 194.3322    1     310
## 23 234.3200    2     310
## 24 232.8416    3     310
## 25 229.3074    4     310

29 / 42

Un modelo con efecto aleatorio en el intercepto:

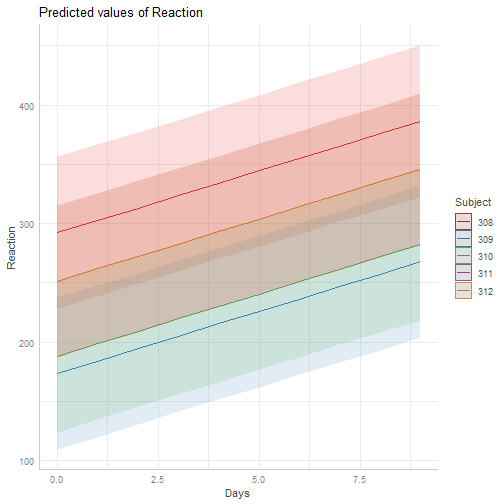
lmod1 = lmer ( Reaction ~ Days + ( 1 | Subject ) , data= sleepstudy )
summary(lmod1)

## Linear mixed model fit by REML ['lmerMod']
## Formula: Reaction ~ Days + (1 | Subject)
##    Data: sleepstudy
## 
## REML criterion at convergence: 1786.5
## 
## Scaled residuals: 
##     Min      1Q  Median      3Q     Max 
## -3.2257 -0.5529  0.0109  0.5188  4.2506 
## 
## Random effects:
##  Groups   Name        Variance Std.Dev.
##  Subject  (Intercept) 1378.2   37.12   
##  Residual              960.5   30.99   
## Number of obs: 180, groups:  Subject, 18
## 
## Fixed effects:
##             Estimate Std. Error t value
## (Intercept) 251.4051     9.7467   25.79
## Days         10.4673     0.8042   13.02
## 
## Correlation of Fixed Effects:
##      (Intr)
## Days -0.371

30 / 42

Un modelo con efecto aleatorio en el intercepto:

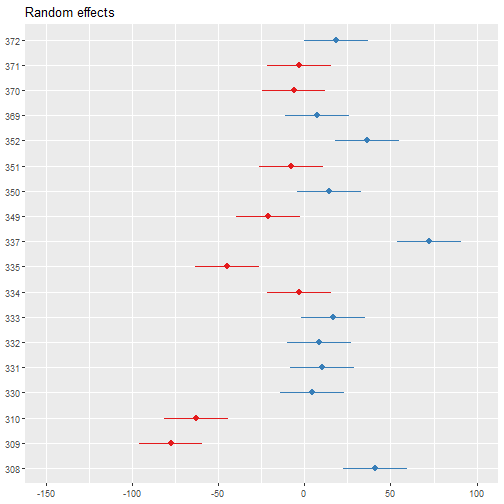
coef(lmod1)$Subject

##     (Intercept)     Days
## 308    292.1888 10.46729
## 309    173.5556 10.46729
## 310    188.2965 10.46729
## 330    255.8115 10.46729
## 331    261.6213 10.46729
## 332    259.6263 10.46729
## 333    267.9056 10.46729
## 334    248.4081 10.46729
## 335    206.1230 10.46729
## 337    323.5878 10.46729
## 349    230.2089 10.46729
## 350    265.5165 10.46729
## 351    243.5429 10.46729
## 352    287.7835 10.46729
## 369    258.4415 10.46729
## 370    245.0424 10.46729
## 371    248.1108 10.46729
## 372    269.5209 10.46729

31 / 42

Un modelo con efecto aleatorio en la pendiente:

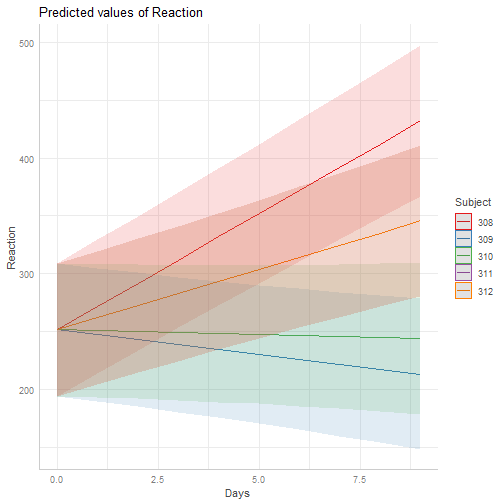
lmod2 = lmer ( Reaction ~ Days + ( 0 + Days | Subject ) , data= sleepstudy )
summary(lmod2)

## Linear mixed model fit by REML ['lmerMod']
## Formula: Reaction ~ Days + (0 + Days | Subject)
##    Data: sleepstudy
## 
## REML criterion at convergence: 1766.5
## 
## Scaled residuals: 
##     Min      1Q  Median      3Q     Max 
## -3.5104 -0.5588  0.0541  0.6244  4.6022 
## 
## Random effects:
##  Groups   Name Variance Std.Dev.
##  Subject  Days  52.71    7.26   
##  Residual      842.03   29.02   
## Number of obs: 180, groups:  Subject, 18
## 
## Fixed effects:
##             Estimate Std. Error t value
## (Intercept)   251.41       4.02  62.539
## Days           10.47       1.87   5.599
## 
## Correlation of Fixed Effects:
##      (Intr)
## Days -0.340

32 / 42

Un modelo con efecto aleatorio en la pendiente:

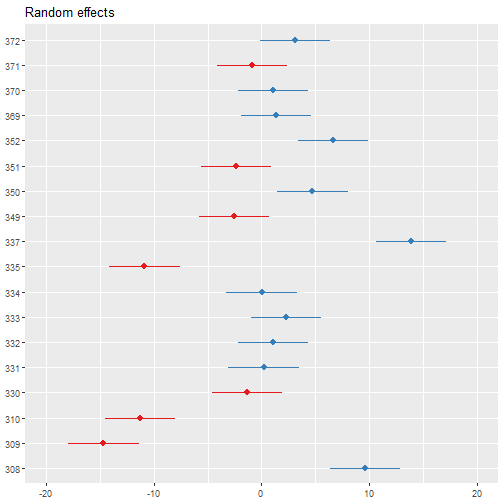
coef(lmod2)$Subject

##     (Intercept)       Days
## 308    251.4051 20.0866918
## 309    251.4051 -4.2326711
## 310    251.4051 -0.8189202
## 330    251.4051  9.1273878
## 331    251.4051 10.6754843
## 332    251.4051 11.5352979
## 333    251.4051 12.7430088
## 334    251.4051 10.4774867
## 335    251.4051 -0.4337385
## 337    251.4051 24.3577325
## 349    251.4051  7.9069248
## 350    251.4051 15.2012144
## 351    251.4051  8.1041559
## 352    251.4051 17.1349527
## 369    251.4051 11.8340809
## 370    251.4051 11.5298510
## 371    251.4051  9.5898795
## 372    251.4051 13.5923281

33 / 42

Un modelo con efecto aleatorio en el intercepto y la pendiente:

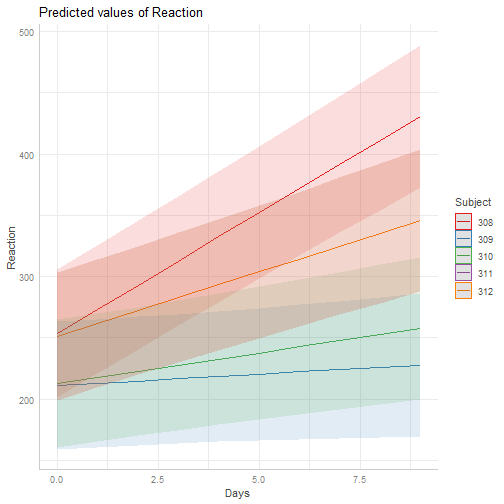
lmod3 = lmer ( Reaction ~ Days + ( Days | Subject ) , data= sleepstudy )
summary(lmod3)

## Linear mixed model fit by REML ['lmerMod']
## Formula: Reaction ~ Days + (Days | Subject)
##    Data: sleepstudy
## 
## REML criterion at convergence: 1743.6
## 
## Scaled residuals: 
##     Min      1Q  Median      3Q     Max 
## -3.9536 -0.4634  0.0231  0.4634  5.1793 
## 
## Random effects:
##  Groups   Name        Variance Std.Dev. Corr
##  Subject  (Intercept) 612.10   24.741       
##           Days         35.07    5.922   0.07
##  Residual             654.94   25.592       
## Number of obs: 180, groups:  Subject, 18
## 
## Fixed effects:
##             Estimate Std. Error t value
## (Intercept)  251.405      6.825  36.838
## Days          10.467      1.546   6.771
## 
## Correlation of Fixed Effects:
##      (Intr)
## Days -0.138

34 / 42

Un modelo con efecto aleatorio en el intercepto y la pendiente:

coef(lmod3)$Subject

##     (Intercept)       Days
## 308    253.6637 19.6662617
## 309    211.0064  1.8476053
## 310    212.4447  5.0184295
## 330    275.0957  5.6529356
## 331    273.6654  7.3973743
## 332    260.4447 10.1951090
## 333    268.2456 10.2436499
## 334    244.1725 11.5418676
## 335    251.0714 -0.2848792
## 337    286.2956 19.0955511
## 349    226.1949 11.6407181
## 350    238.3351 17.0815038
## 351    255.9830  7.4520239
## 352    272.2688 14.0032871
## 369    254.6806 11.3395008
## 370    225.7921 15.2897709
## 371    252.2122  9.4791297
## 372    263.7197 11.7513080

35 / 42

Resultados

Efectos aleatorios (intercepto en modelo 1):

sjPlot::plot_model(lmod1, type = 're')

36 / 42

Resultados

Efectos aleatorios (pendiente en modelo 2):

sjPlot::plot_model(lmod2, type = 're')

37 / 42

Resultados

Para cinco niveles del efecto aleatorio (variable Subject):

myRandom1 = ggpredict(model = lmod1, type = 're', terms = c('Days', 'Subject [308,309,310,311,312]'))
plot(myRandom1)

38 / 42

Resultados

Para cinco niveles del efecto aleatorio (variable Subject):

myRandom2 = ggpredict(model = lmod2, type = 're', terms = c('Days', 'Subject [308,309,310,311,312]'))
plot(myRandom2)

39 / 42

Resultados

Para cinco niveles del efecto aleatorio (variable Subject):

myRandom3 = ggpredict(model = lmod3, type = 're', terms = c('Days', 'Subject [308,309,310,311,312]'))
plot(myRandom3)

40 / 42

Resultados

sjPlot::tab_model(lmod1)

	Reaction
Predictors	Estimates	CI	p
(Intercept)	251.41	232.17 – 270.64	<0.001
Days	10.47	8.88 – 12.05	<0.001
Random Effects
σ²	960.46
τ₀₀ _Subject	1378.18
ICC	0.59
N _Subject	18
Observations	180
Marginal R² / Conditional R²	0.280 / 0.704

41 / 42

Resultados

sjPlot::tab_model(lmod1)

	Reaction
Predictors	Estimates	CI	p
(Intercept)	251.41	232.17 – 270.64	<0.001
Days	10.47	8.88 – 12.05	<0.001
Random Effects
σ²	960.46
τ₀₀ _Subject	1378.18
ICC	0.59
N _Subject	18
Observations	180
Marginal R² / Conditional R²	0.280 / 0.704

ICC cercano a cero nos sugiere que un modelo con efectos aleatorios no es necesario.

41 / 42

Gracias!

Contacto: cursos@cousteau-group.com

42 / 42

↑, ←, Pg Up, k	Go to previous slide
↓, →, Pg Dn, Space, j	Go to next slide
Home	Go to first slide
End	Go to last slide
Number + Return	Go to specific slide
b / m / f	Toggle blackout / mirrored / fullscreen mode
c	Clone slideshow
p	Toggle presenter mode
t	Restart the presentation timer
?, h	Toggle this help

AlwaysR, Módulo III: Estadística en R

Clase 4: Modelos lineales II. Efectos aleatorios.

Dr. Giancarlo M. Correa

Modelos lineales II

Librerías a utilizar

Problemas con datos

Multicolinealidad

Problemas con datos

Multicolinealidad

Problemas con datos

Multicolinealidad

Problemas con datos

Problemas con datos

Problemas con datos

Problemas con datos

Problemas con datos

Datos faltantes

Datos faltantes

Datos faltantes

Datos faltantes

Datos faltantes

Datos faltantes

Método de supresión

Método de retención

Método de retención

Selección de modelos

Selección de modelos

Selección de modelos

Selección de modelos

Selección de modelos

Selección de modelos

Selección de modelos

Selección de modelos

Selección de modelos

Limitaciones

Selección de modelos

Selección de modelos

Problemas con supuestos

Problemas con supuestos

Linealidad de la asociación

Problemas con supuestos

Linealidad de la asociación

Independencia

Problemas con supuestos

Linealidad de la asociación

Independencia

Normalidad

Transformaciones

Transformaciones

Transformaciones

Transformaciones

Transformaciones

Efectos aleatorios

Efectos aleatorios

Efectos aleatorios

Efectos aleatorios

Efectos aleatorios

Efectos aleatorios

Efectos aleatorios

Efectos aleatorios

Resultados

Resultados

Resultados

Resultados

Resultados

Resultados

Resultados

Gracias!

Modelos lineales II

Help