AlwaysR, Módulo III: Estadística en R
Clase 5: Introducción a modelos lineales y aditivos generalizados (GLM y GAM)
Dr. Giancarlo M. Correa

Modelos lineales generalizados (GLM)
GLM
Un modelo lineal simple puede ser expresado como:
y∼N(μ,σ2)
μ=β0+β1x1+β2x2+...+βpxp
Un GLM es una opción cuando la varianza de la variable respuesta no es constante o no está normalmente distribuida.
GLM transforma la variable respuesta para que el método de estimación de parámetros siga funcionando bien (mediante una función link).
GLM
Un modelo lineal simple puede ser expresado como:
y∼N(μ,σ2)
μ=β0+β1x1+β2x2+...+βpxp
Un GLM es una opción cuando la varianza de la variable respuesta no es constante o no está normalmente distribuida.
GLM transforma la variable respuesta para que el método de estimación de parámetros siga funcionando bien (mediante una función link).
Al momento de implementar un GLM, debemos decidir dos cosas:
- La distribución a utilizar
- La función link (esto normalmente está por defecto en R).
y∼EDM(μ,etc)
g(μ)=β0+p∑j=1βjxj
GLM
Por ejemplo, podemos tener:
data(quilpie)head(quilpie)## Year Rain SOI Phase Exceed y## 1 1921 38.4 2.7 2 Yes 1## 2 1922 0.0 2.0 5 No 0## 3 1923 0.0 -10.7 3 No 0## 4 1924 24.4 6.9 2 Yes 1## 5 1925 0.0 -12.5 3 No 0## 6 1926 9.1 -1.0 4 No 0Para este caso, si y es la variable respuesta, entonces podemos usar:
yi∼Binom(μi,mi)
logμi1−μi=β0+β1SOIi
GLM: respuesta binaria
Para una variable de respuesta binaria (e.g. 0/1 - presencia/asusencia - hembra/macho), tipicamente la modelamos con una función link tipo logit y función de varianza μ(1−μ). La respuesta modelada son las probabilidades de registro predichas (predicted log odds) del evento de interés.
GLM: respuesta binaria
Para una variable de respuesta binaria (e.g. 0/1 - presencia/asusencia - hembra/macho), tipicamente la modelamos con una función link tipo logit y función de varianza μ(1−μ). La respuesta modelada son las probabilidades de registro predichas (predicted log odds) del evento de interés.
head(hsb)## id gender race ses schtyp prog read write math science socst## 1 70 male white low public general 57 52 41 47 57## 2 121 female white middle public vocation 68 59 53 63 61## 3 86 male white high public general 44 33 54 58 31## 4 141 male white high public vocation 63 44 47 53 56## 5 172 male white middle public academic 47 52 57 53 61## 6 113 male white middle public academic 44 52 51 63 61GLM: respuesta binaria
Para una variable de respuesta binaria (e.g. 0/1 - presencia/asusencia - hembra/macho), tipicamente la modelamos con una función link tipo logit y función de varianza μ(1−μ). La respuesta modelada son las probabilidades de registro predichas (predicted log odds) del evento de interés.
head(hsb)## id gender race ses schtyp prog read write math science socst## 1 70 male white low public general 57 52 41 47 57## 2 121 female white middle public vocation 68 59 53 63 61## 3 86 male white high public general 44 33 54 58 31## 4 141 male white high public vocation 63 44 47 53 56## 5 172 male white middle public academic 47 52 57 53 61## 6 113 male white middle public academic 44 52 51 63 61Para este ejemplo, modelaremos el registro de hsb$prog == academic.
GLM: respuesta binaria
En R vamos a usar:
hsb$obj_var = ifelse(test = hsb$prog == 'academic', yes = 1, no = 0)mod1 = glm(obj_var ~ read, family = binomial, data = hsb)Aquí, la variable respuesta es una variable indicadora (binaria):
hsb$obj_var[1:20]## [1] 0 0 0 0 1 1 0 1 0 1 0 1 1 1 1 0 1 0 1 0summary(mod1)## ## Call:## glm(formula = obj_var ~ read, family = binomial, data = hsb)## ## Deviance Residuals: ## Min 1Q Median 3Q Max ## -1.8817 -1.0329 0.4935 1.0182 1.8654 ## ## Coefficients:## Estimate Std. Error z value Pr(>|z|) ## (Intercept) -4.67739 0.90426 -5.173 2.31e-07 ***## read 0.09207 0.01730 5.321 1.03e-07 ***## ---## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1## ## (Dispersion parameter for binomial family taken to be 1)## ## Null deviance: 276.76 on 199 degrees of freedom## Residual deviance: 241.58 on 198 degrees of freedom## AIC: 245.58## ## Number of Fisher Scoring iterations: 4GLM: respuesta binaria
Vemos un par de términos nuevos:
Null deviance: nos indica que tan bien la variable respuesta puede ser predicha por un modelo que solo contenga el intercepto. Un valor pequeño nos indica que el modelo explica muy bien la variable respuesta.
Residual deviance: nos indica que tan bien la variable respuesta es predicha por el modelo implementado. Un valor pequeño nos indica que el modelo explica muy bien la variable respuesta.
GLM: respuesta binaria
Vemos un par de términos nuevos:
Null deviance: nos indica que tan bien la variable respuesta puede ser predicha por un modelo que solo contenga el intercepto. Un valor pequeño nos indica que el modelo explica muy bien la variable respuesta.
Residual deviance: nos indica que tan bien la variable respuesta es predicha por el modelo implementado. Un valor pequeño nos indica que el modelo explica muy bien la variable respuesta.
Se recomienda explorar ?family para conocer las funciones link de cada distribución.
mod2 = glm(Students ~ Days, family = poisson, data = cases)summary(mod2)## ## Call:## glm(formula = Students ~ Days, family = poisson, data = cases)## ## Deviance Residuals: ## Min 1Q Median 3Q Max ## -2.00482 -0.85719 -0.09331 0.63969 1.73696 ## ## Coefficients:## Estimate Std. Error z value Pr(>|z|) ## (Intercept) 1.990235 0.083935 23.71 <2e-16 ***## Days -0.017463 0.001727 -10.11 <2e-16 ***## ---## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1## ## (Dispersion parameter for poisson family taken to be 1)## ## Null deviance: 215.36 on 108 degrees of freedom## Residual deviance: 101.17 on 107 degrees of freedom## AIC: 393.11## ## Number of Fisher Scoring iterations: 5mod3 = glm(count ~ year + yearSqr, family = "poisson", data = disc)summary(mod3)## ## Call:## glm(formula = count ~ year + yearSqr, family = "poisson", data = disc)## ## Deviance Residuals: ## Min 1Q Median 3Q Max ## -2.9066 -0.8397 -0.2544 0.4776 3.3303 ## ## Coefficients:## Estimate Std. Error z value Pr(>|z|) ## (Intercept) 7.592e-01 1.814e-01 4.186 2.84e-05 ***## year 3.356e-02 8.499e-03 3.948 7.87e-05 ***## yearSqr -4.106e-04 8.699e-05 -4.720 2.35e-06 ***## ---## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1## ## (Dispersion parameter for poisson family taken to be 1)## ## Null deviance: 164.68 on 99 degrees of freedom## Residual deviance: 132.84 on 97 degrees of freedom## AIC: 407.85## ## Number of Fisher Scoring iterations: 5mod4 = glm(count ~ year + yearSqr, family = "quasipoisson", data = disc)summary(mod4)## ## Call:## glm(formula = count ~ year + yearSqr, family = "quasipoisson", ## data = disc)## ## Deviance Residuals: ## Min 1Q Median 3Q Max ## -2.9066 -0.8397 -0.2544 0.4776 3.3303 ## ## Coefficients:## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 0.7592473 0.2072715 3.663 0.000406 ***## year 0.0335569 0.0097112 3.455 0.000816 ***## yearSqr -0.0004106 0.0000994 -4.131 7.66e-05 ***## ---## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1## ## (Dispersion parameter for quasipoisson family taken to be 1.305649)## ## Null deviance: 164.68 on 99 degrees of freedom## Residual deviance: 132.84 on 97 degrees of freedom## AIC: NA## ## Number of Fisher Scoring iterations: 5GLM: binomial negativa
mod5 = MASS::glm.nb(count ~ year + yearSqr, data = disc)summary(mod5)## ## Call:## MASS::glm.nb(formula = count ~ year + yearSqr, data = disc, init.theta = 11.53157519, ## link = log)## ## Deviance Residuals: ## Min 1Q Median 3Q Max ## -2.6849 -0.7707 -0.2344 0.4232 2.7134 ## ## Coefficients:## Estimate Std. Error z value Pr(>|z|) ## (Intercept) 7.526e-01 2.019e-01 3.727 0.000194 ***## year 3.386e-02 9.471e-03 3.575 0.000350 ***## yearSqr -4.132e-04 9.627e-05 -4.292 1.77e-05 ***## ---## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1## ## (Dispersion parameter for Negative Binomial(11.5316) family taken to be 1)## ## Null deviance: 131.91 on 99 degrees of freedom## Residual deviance: 106.20 on 97 degrees of freedom## AIC: 406.21## ## Number of Fisher Scoring iterations: 1## ## ## Theta: 11.53 ## Std. Err.: 7.42 ## ## 2 x log-likelihood: -398.214GLM: respuesta gamma
Dada nuestra base de datos:
head(case1202)## Bsal Sal77 Sex Senior Age Educ Exper## 1 5040 12420 Male 96 329 15 14.0## 2 6300 12060 Male 82 357 15 72.0## 3 6000 15120 Male 67 315 15 35.5## 4 6000 16320 Male 97 354 12 24.0## 5 6000 12300 Male 66 351 12 56.0## 6 6840 10380 Male 92 374 15 41.5GLM: respuesta gamma
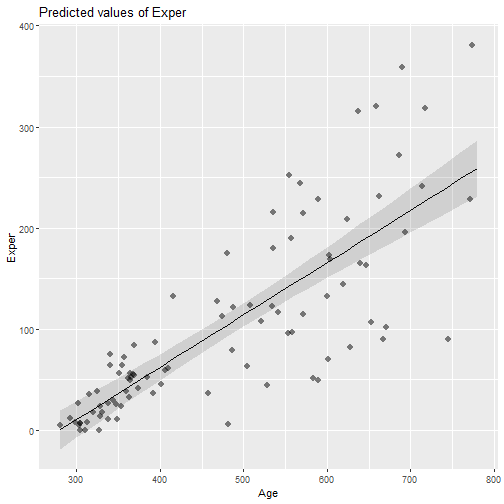
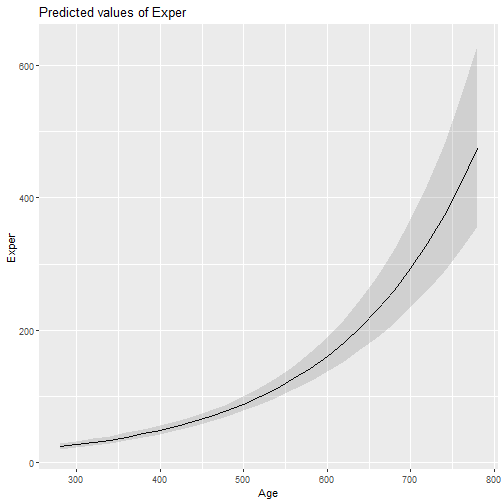
Modelo lineal simple:
mod6 = lm(Exper ~ Age, data=case1202)summary(mod6)## ## Call:## lm(formula = Exper ~ Age, data = case1202)## ## Residuals:## Min 1Q Median 3Q Max ## -150.974 -21.633 -3.205 24.866 146.490 ## ## Coefficients:## Estimate Std. Error t value Pr(>|t|) ## (Intercept) -144.59165 20.26830 -7.134 2.28e-10 ***## Age 0.51754 0.04099 12.626 < 2e-16 ***## ---## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1## ## Residual standard error: 55.13 on 91 degrees of freedom## Multiple R-squared: 0.6366, Adjusted R-squared: 0.6326 ## F-statistic: 159.4 on 1 and 91 DF, p-value: < 2.2e-16summary(mod7)## ## Call:## glm(formula = Exper + 1 ~ Age, family = Gamma(link = "log"), ## data = case1202)## ## Deviance Residuals: ## Min 1Q Median 3Q Max ## -2.22397 -0.60604 -0.02406 0.34153 1.07844 ## ## Coefficients:## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 1.4770108 0.2118855 6.971 4.87e-10 ***## Age 0.0060060 0.0004285 14.016 < 2e-16 ***## ---## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1## ## (Dispersion parameter for Gamma family taken to be 0.3321014)## ## Null deviance: 101.471 on 92 degrees of freedom## Residual deviance: 46.044 on 91 degrees of freedom## AIC: 970.8## ## Number of Fisher Scoring iterations: 6Modelos aditivos generalizados (GAM)
GAM
Hay casos en donde la asociación lineal entre las variables no se cumple. Para casos donde no se tenga una relación lineal entre la variable respuesta y variables independientes, podemos utilizar un modelo aditivo generalizado:
y∼EDM(μ,etc)
g(μ)=β0+f(x1)+f(x2)+...+f(xp)
E(y)∼μ Variables independientes ahora incorporan una función de suavizamiento (basis function, f ), lo que permite relaciones no lineales entre las variables.
GAM en R
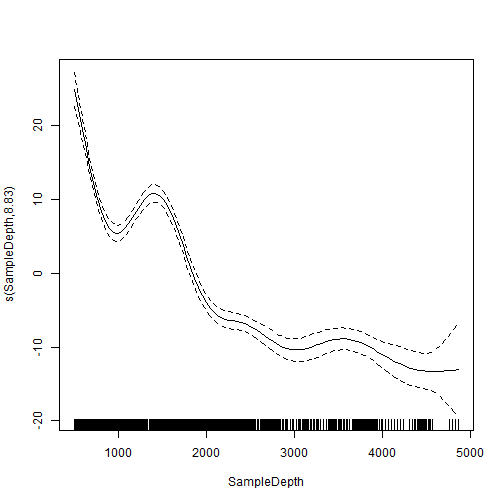
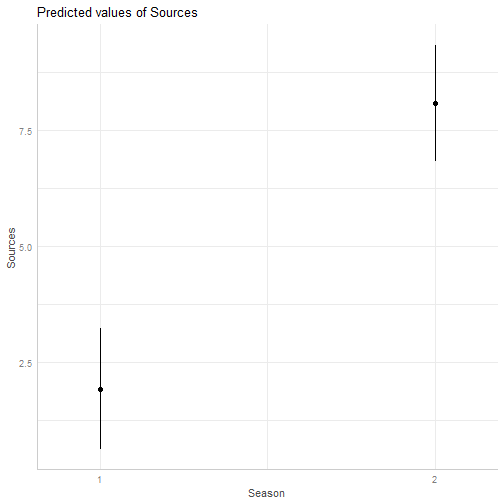
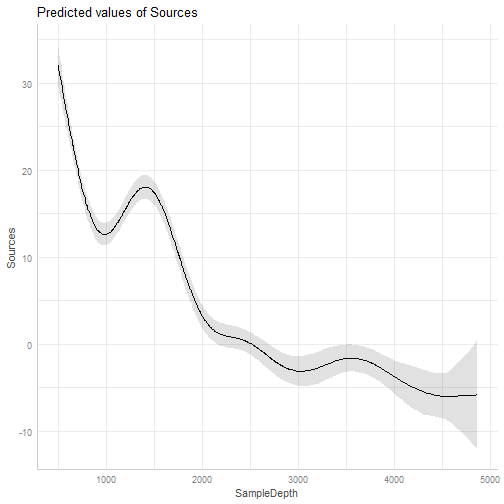
library(mgcv)## This is mgcv 1.8-42. For overview type 'help("mgcv-package")'.isit = read.csv('ISIT.csv')isit$Season <- as.factor(isit$Season)head(isit)## SampleDepth Sources Station Time Latitude Longitude Xkm Ykm Month Year## 1 517 28.73 1 3 50.1508 -14.4792 -34.106 16.779 4 2001## 2 582 27.90 1 3 50.1508 -14.4792 -34.106 16.779 4 2001## 3 547 23.44 1 3 50.1508 -14.4792 -34.106 16.779 4 2001## 4 614 18.33 1 3 50.1508 -14.4792 -34.106 16.779 4 2001## 5 1068 12.38 1 3 50.1508 -14.4792 -34.106 16.779 4 2001## 6 1005 11.23 1 3 50.1508 -14.4792 -34.106 16.779 4 2001## BottomDepth Season Discovery RelativeDepth## 1 3939 1 252 3422## 2 3939 1 252 3357## 3 3939 1 252 3392## 4 3939 1 252 3325## 5 3939 1 252 2871## 6 3939 1 252 2934fit_gam = gam(Sources ~ Season + s(SampleDepth), data = isit)summary(fit_gam)## ## Family: gaussian ## Link function: identity ## ## Formula:## Sources ~ Season + s(SampleDepth)## ## Parametric coefficients:## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 7.2493 0.3613 20.07 <2e-16 ***## Season2 6.1631 0.4826 12.77 <2e-16 ***## ---## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1## ## Approximate significance of smooth terms:## edf Ref.df F p-value ## s(SampleDepth) 8.829 8.991 184.6 <2e-16 ***## ---## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1## ## R-sq.(adj) = 0.692 Deviance explained = 69.5%## GCV = 42.991 Scale est. = 42.401 n = 789GAM en R
Aquí hay algunos términos nuevos:
edf: effective degrees of freedom. Es un resultados de la penalidad aplicada al grado de suavizamiento (detalles estadísticos en bibliografía!). Evita un over-suavizamiento o under-suavizamiento. Puede interpretarse como el nivel de suavizamiento aplicado a una variable.
GCV: generalized cross validation. Es un proxy del error de predicción cuadrático medio (mean square prediction error). Esto se basa en un método llamado leave-one-out cross validation. Utilizado para comparar modelos (similar a AIC), donde el modelo con menor GCV es el mejor.
Deviance explained: es una generalización del R2 (sin ajustar).
Scale est.: equivalente a la suma de cuadrado de los residuales.
GAM en R
Existen diferentes formas de suavizar una variable (smooth term), los cuales pueden ser explorados aquí. El método por defecto es: thin plate regression splines (funciona bien en la mayoría de los casos) bs = "tp".
También debemos revisar los supuestos de un GAM:
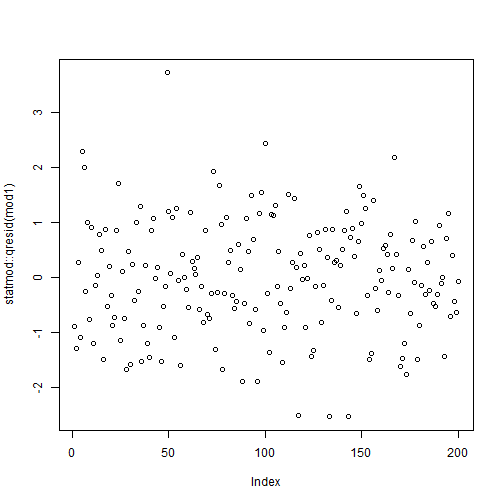
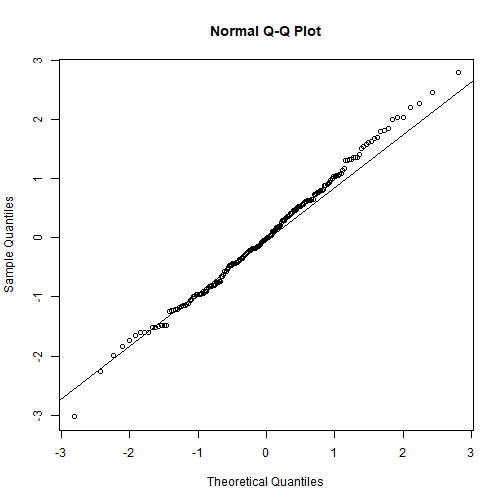
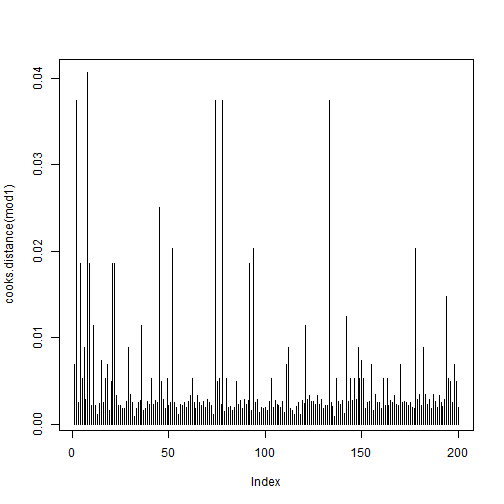
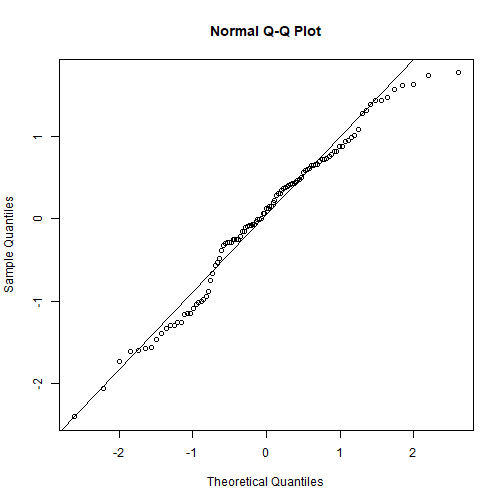
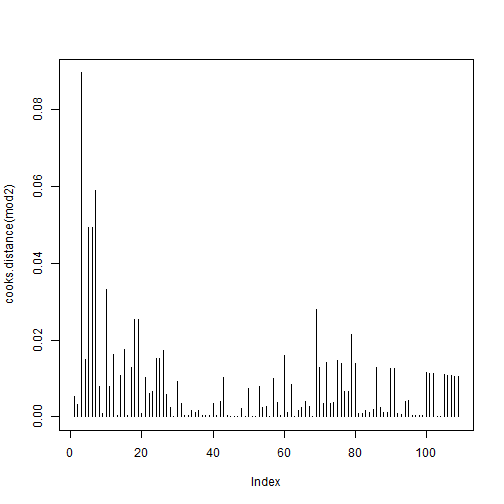
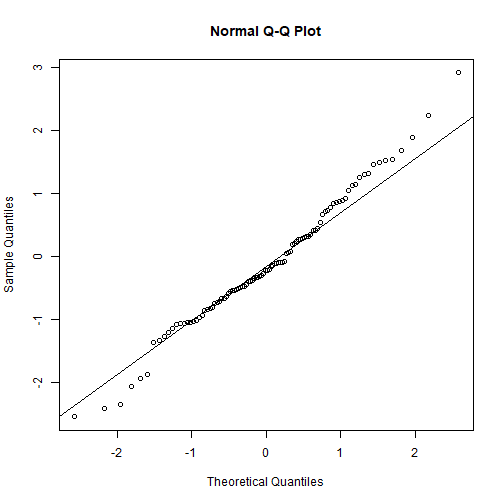
par(mfrow = c(2,2))gam.check(fit_gam)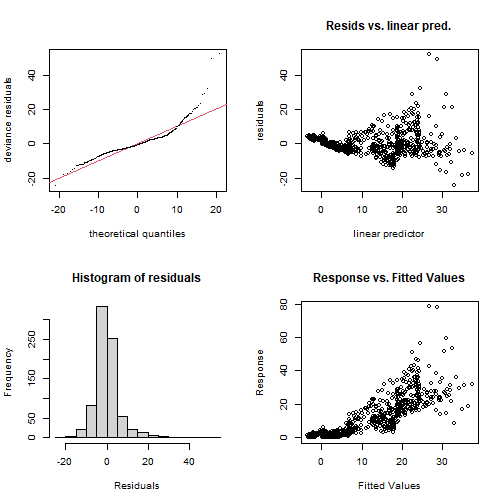
## ## Method: GCV Optimizer: magic## Smoothing parameter selection converged after 9 iterations.## The RMS GCV score gradient at convergence was 0.0002508607 .## The Hessian was positive definite.## Model rank = 11 / 11 ## ## Basis dimension (k) checking results. Low p-value (k-index<1) may## indicate that k is too low, especially if edf is close to k'.## ## k' edf k-index p-value## s(SampleDepth) 9.00 8.83 1.1 1También revisamos el nivel de suavizamiento que hemos usado usando gam.check(). Es decir, el número de nodos (k) en la función s(). Recuerden que el valor por defecto es s(..., k = 10).
## k' edf k-index p-value## s(SampleDepth) 9 8.82882 1.10425 1Lo mas importante es ver el p−value. Un valor p−value muy pequeño nos dice que no hemos usado un k suficientemente alto.
GAM en R: respuesta binomial
Hasta el momento hemos visto una respuesta Gaussiana (normal) con una función link igual a la identidad (identity). En GAMs también podemos incorporar diferentes familias:
cricketer = read.csv('cricketr.csv')cricketer$hand = NAcricketer$hand = ifelse(test = cricketer$left == 'left', yes = 1, no = 0)head(cricketer)## left year life dead acd kia inbed cause hand## 1 right 1890 102 0 0 0 0 alive 0## 2 left 1892 100 0 0 0 0 alive 1## 3 right 1893 99 0 0 0 0 alive 0## 4 right 1894 98 0 0 0 0 alive 0## 5 right 1896 96 0 0 0 0 alive 0## 6 right 1896 96 0 0 0 0 alive 0Para implementar el modelo:
hand.gam = gam(hand ~ s(year), data=cricketer, family=binomial)summary(hand.gam)## ## Family: binomial ## Link function: logit ## ## Formula:## hand ~ s(year)## ## Parametric coefficients:## Estimate Std. Error z value Pr(>|z|) ## (Intercept) -1.49285 0.03361 -44.41 <2e-16 ***## ---## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1## ## Approximate significance of smooth terms:## edf Ref.df Chi.sq p-value ## s(year) 7.873 8.664 23.87 0.0066 **## ---## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1## ## R-sq.(adj) = 0.00301 Deviance explained = 0.472%## UBRE = -0.044557 Scale est. = 1 n = 5960GAM en R: respuesta Poisson
Podemos transformar los datos de la siguiente forma:
rtlef = data.frame(with(cricketer, as(table(year, left),"matrix")))rtlef$year = as.numeric(rownames(rtlef))head(rtlef)## left right year## 1840 1 6 1840## 1841 4 16 1841## 1842 5 16 1842## 1843 3 25 1843## 1844 4 25 1844## 1845 2 24 1845GAM en R: respuesta Poisson
Podemos transformar los datos de la siguiente forma:
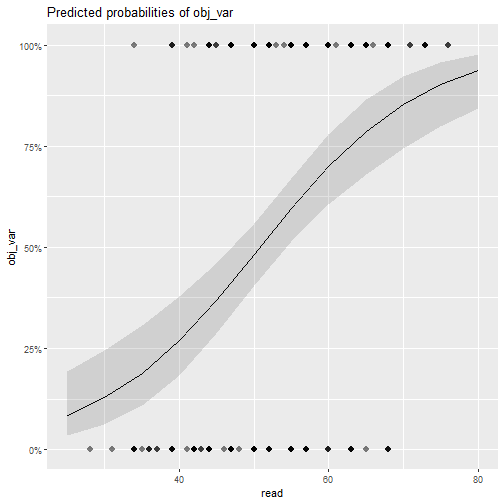
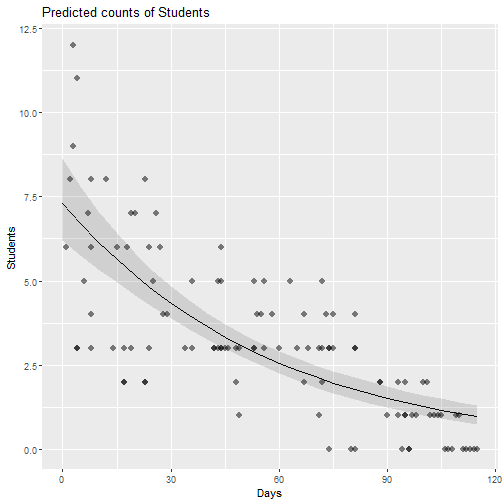
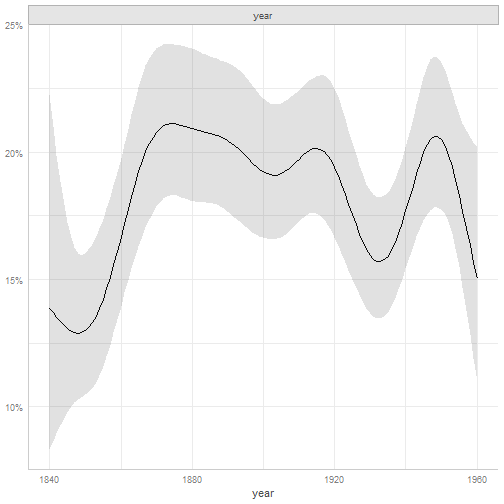
rtlef = data.frame(with(cricketer, as(table(year, left),"matrix")))rtlef$year = as.numeric(rownames(rtlef))head(rtlef)## left right year## 1840 1 6 1840## 1841 4 16 1841## 1842 5 16 1842## 1843 3 25 1843## 1844 4 25 1844## 1845 2 24 1845hand.gam2 = gam(left ~ s(year), data=rtlef, family=poisson)plot(ggeffects::ggpredict(hand.gam2), facets = TRUE)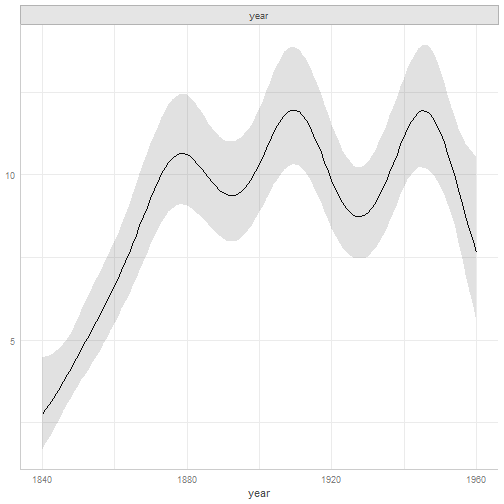
Hay mucha información sobre GAMs. Se recomienda esta fuente.