Modelos avanzados en evaluación de recursos pesqueros
Dr. Giancarlo M. Correa
Cousteau Consultant Group
Modelo poblacional
Estructura interna
Dos principales dimensiones: años y edad.

Haddon (2011)
Crecimiento: estructura inicial
Al nacer, se asigna la talla mínima en la población (Lmin). Luego, crecen linealmente hasta A1:
L0,a=Lmin+ba
Donde
b=LA1−LminA1
- a= edad
- A1= edad de referencia (cercana a la edad 0). Se recomienda que sea la edad donde comenzamos a tener buenos datos
Crecimiento: estructura inicial
Para a>A1, los peces crecen según la ecuación de crecimiento seleccionada
Por ejemplo, usando la ecuación de von Bertalanffy, longitud media a la edad de la población:
L0,a=L∞+(LA1−L∞)(exp(−k(a−A1)))
- LA1= longitud media a la edad A1 (cm)
- L∞= longitud asintótica (cm)
- k= tasa de crecimiento (1/year)
Crecimiento: dinámica
Para y>0, usamos:
Ly+1,a+1=Ly,a+(Ly,a−L∞)(exp(−k)−1)
Para el grupo plus, la ecuación es ligeramente diferente para acumular tallas (ver Technical Description, Methot and Wetzel (2013)).
Crecimiento
Para cualquier fracción θ del año:
˜Ly,a=Ly,a+(Ly,a−L∞)(exp(−kθ)−1)
Esto es importante dado que los peces también crecen dentro de un año.
Crecimiento
Otras parametrizaciones estan disponibles:
- Richards (Richards 1959)
- von Bertalanffy with age-specific K
- Growth cessation (Maunder et al. 2018)
Crecimiento
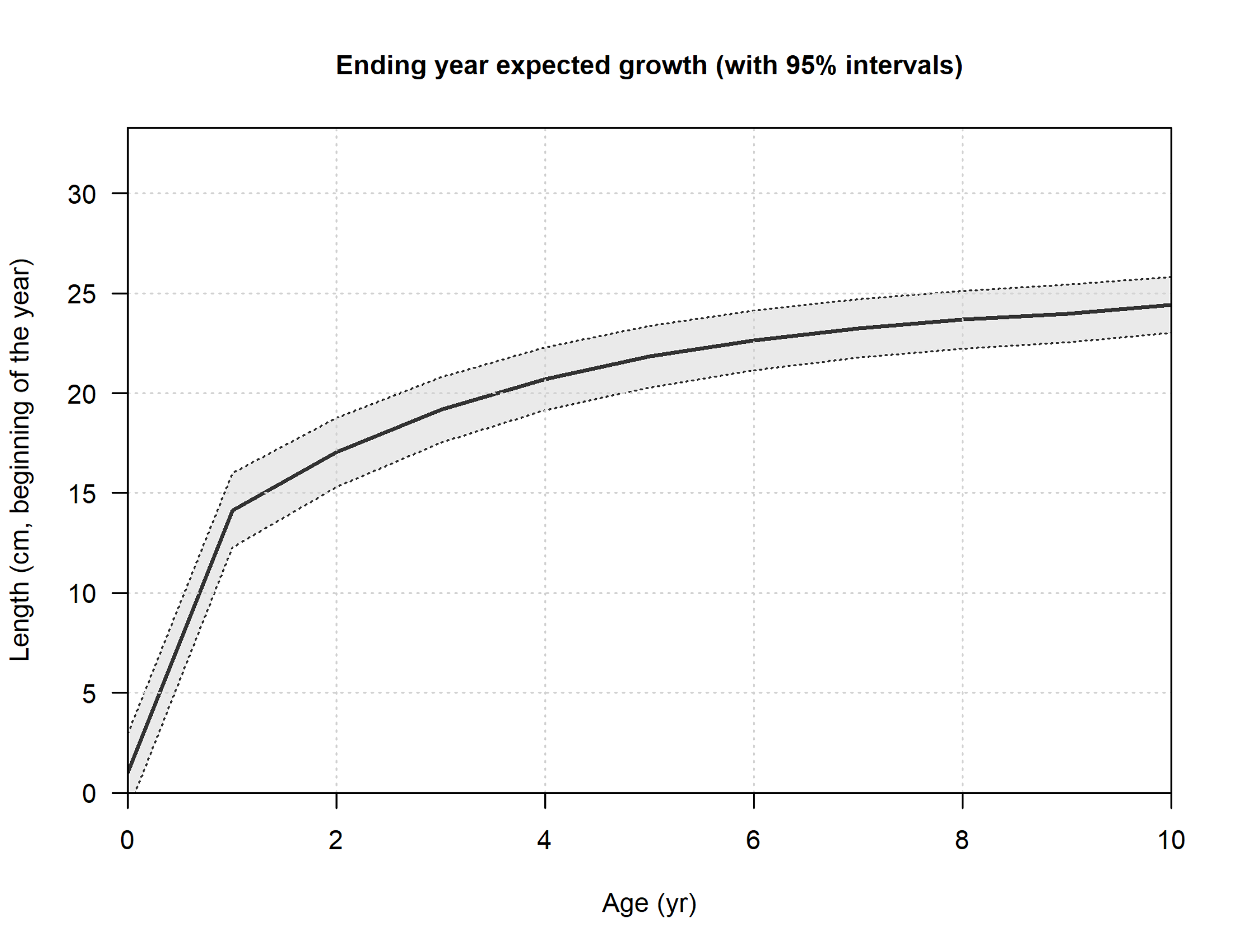
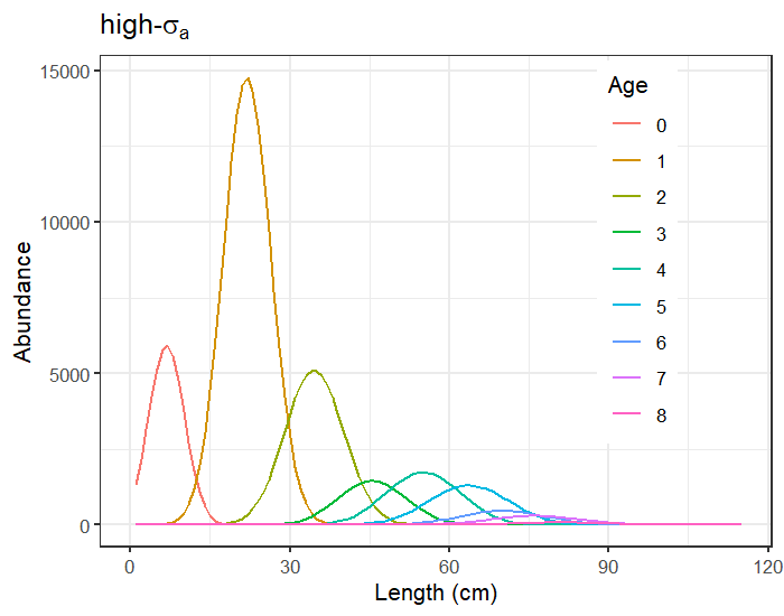
Talla media a la edad de la población.
Crecimiento
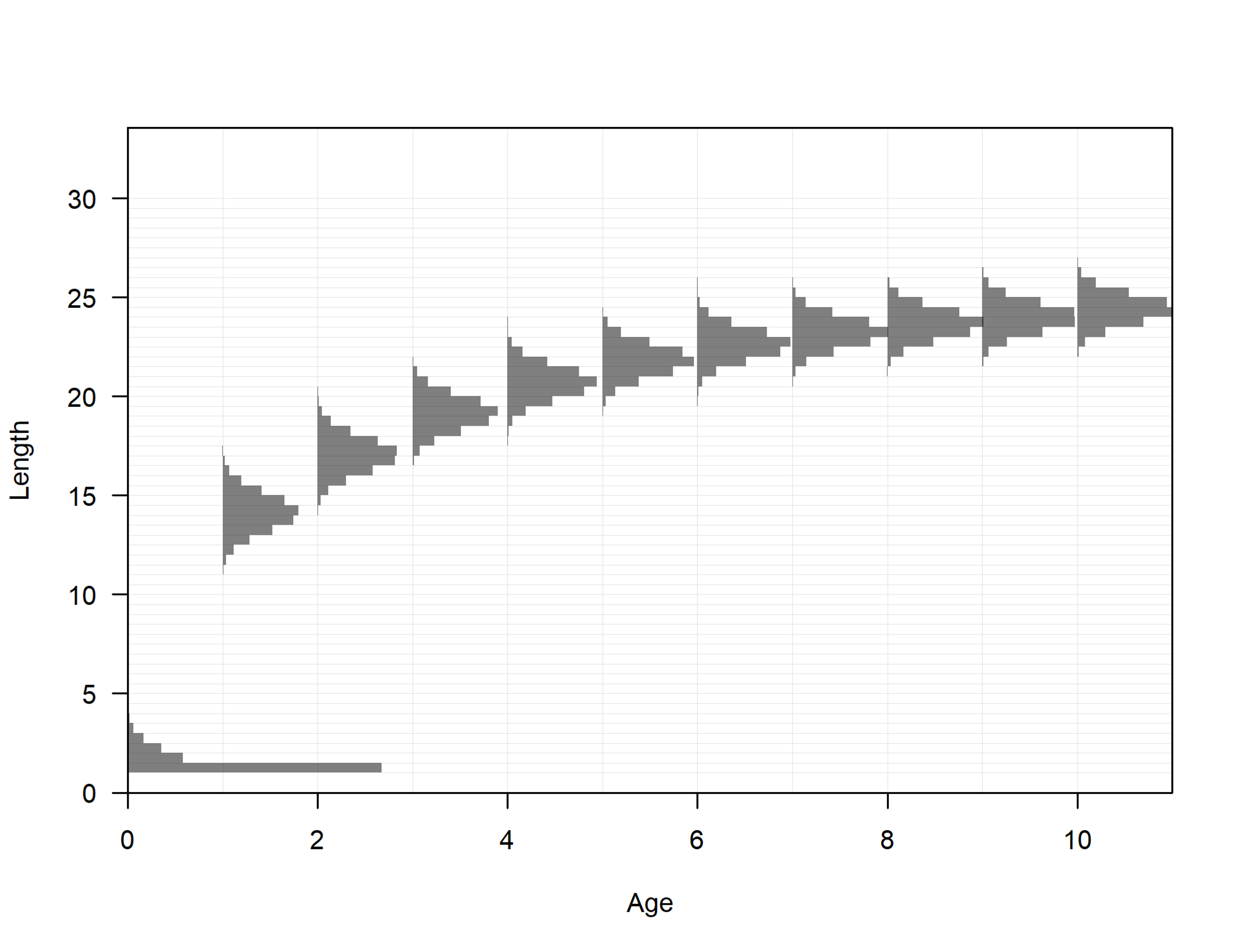
Variabilidad de tallas por edad.
Crecimiento
Variabilidad de tallas por edad:
σy,a={˜Ly,a(CV1)a≤ A1˜Ly,a(CV1+˜Ly,a−L1L2−L1(CV2−CV1))a>A1
Donde tenemos dos parámetros:
- CV1 es el coeficiente de variación de longitudes en la edad A1
- CV2 es el coeficiente de variación de longitudes en la máxima edad
También podemos calcular σy,a como función de la edad.
Matriz de transición
Distribuye la información de cada edad entre las diferentes marcas de clase modeladas.
φy,l,a={Φ(L′min∗−Ly,aσy,a)l=1Φ(L′l+1−Ly,aσy,a)−Φ(L′l−Ly,aσy,a)1<l<nL1−Φ(L′max−Ly,aσy,a)l=nL
Φ es la distribución normal estándar acumulada, L′ representa las marcas de clase modeladas, l es indicador de marca de clase, nL es el número de marcas de clase. L también podría ser ˜L.
Matriz de transición
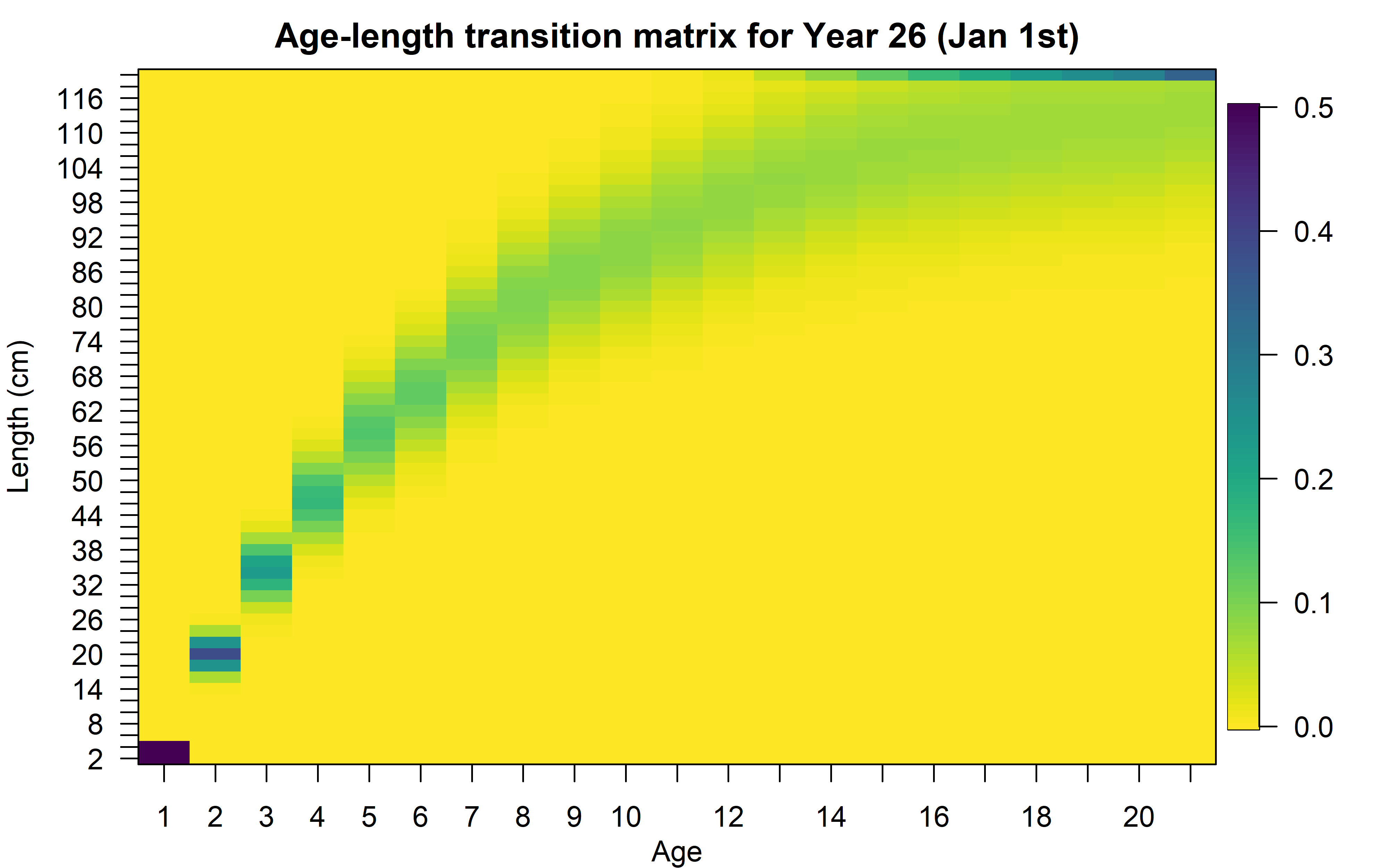
Matriz de transición
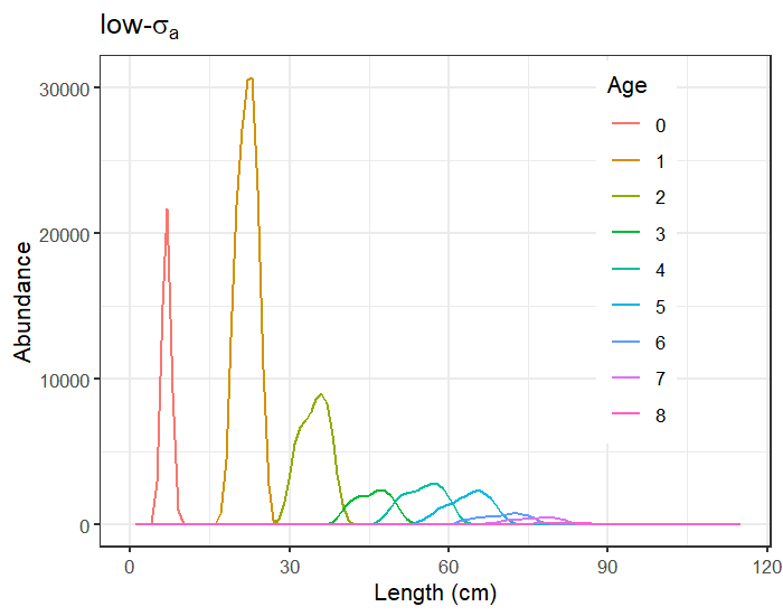
Crecimiento
También podemos modelar morphs, que son colecciones de peces de una cohorte con carácterísticas biológicas únicas (e.g., mortalidad, crecimiento). Usado cuando queremos modelar, por ejemplo, diferentes parámetros biológicos en diferentes áreas o seasons.
Estos morphs a su vez pueden ser dividos en platoons para permitir supervivencia dependiente de la talla. Ver este artículo: McGarvey et al. (2024).
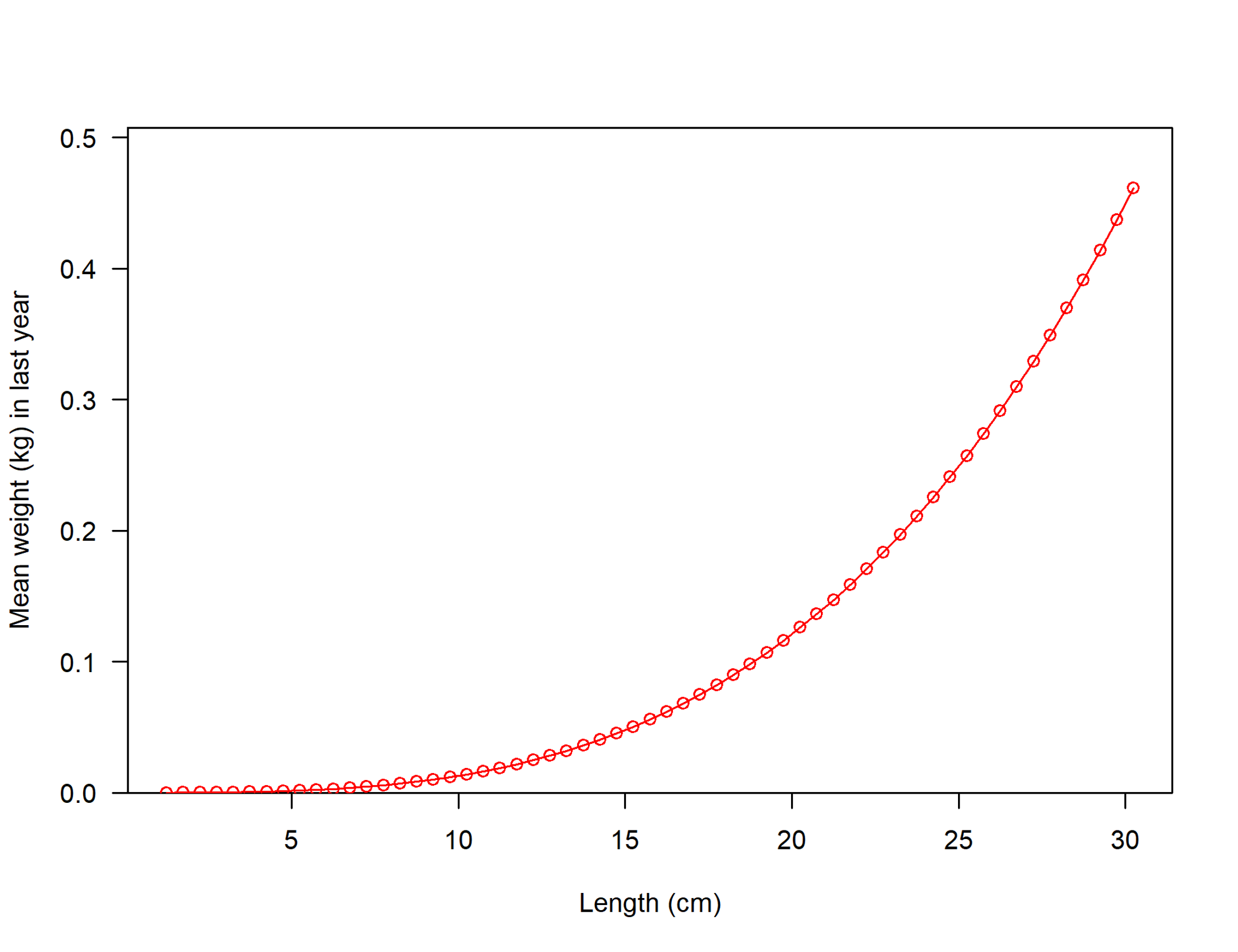
Longitud-peso
Convertir de talla (cm) a peso corporal (kg):
wl=Ω1(L′l)Ω2
Donde Ω1 y Ω2 son parámetros del modelo.
Longitud-peso
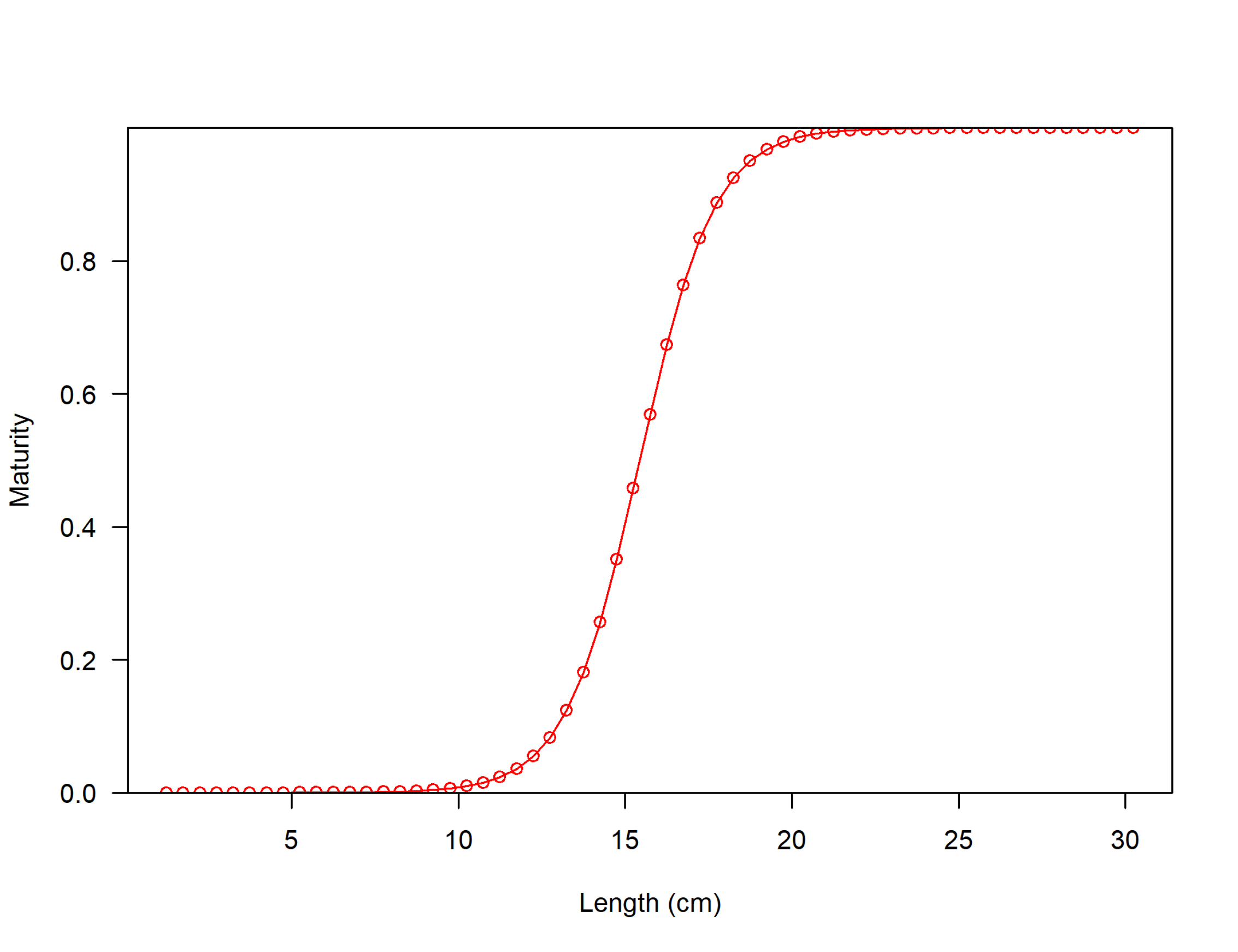
Madurez sexual
Puede ser modelada como una función de talla o edad. Como función de talla:
Matl=11+exp(Ω4(L′l−Ω3))
Donde Ω3 (talla a 50% madurez) y Ω4 (pendiente) son parámetros del modelo.
Madurez sexual
Producción de huevos
La producción de huevos es modelada como una función de la talla:
Eggsl=Ω5+wlΩ6
Donde Eggsl representa la producción de huevos por kg de peso de la hembra. Donde Ω5 y Ω6 son parámetros del modelo.
Producción de huevos
Asumiendo Ω5=1 y Ω6=0:
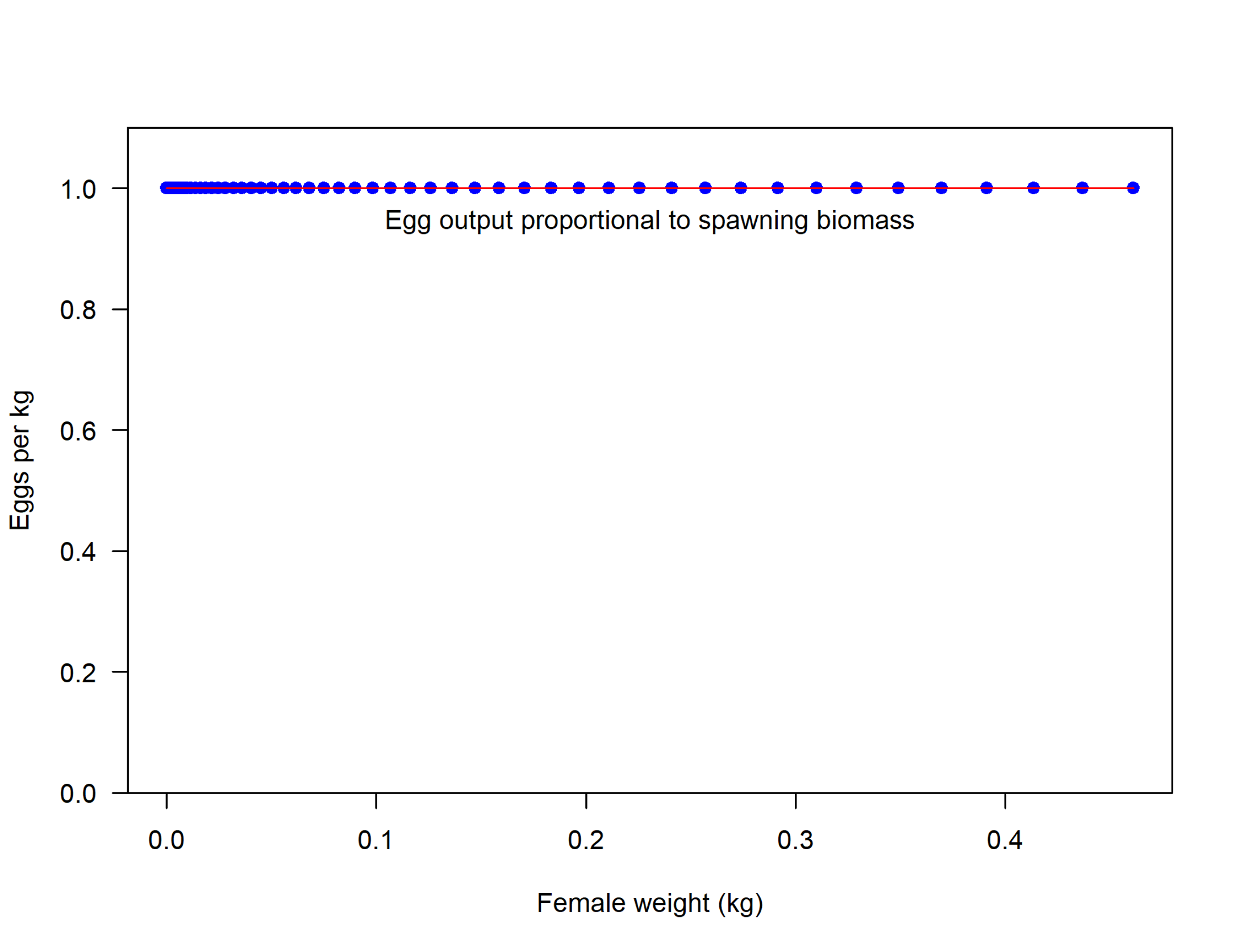
Fecunidad
Es modelada como:
fy,a=∑lφy,l,a(MatlEggslwl)
Finalmente, la biomasa desovante (SSB) puede ser estimada como:
SSBy=∑aNy,afy,a
Stock-reclutamiento
Usando la función Berverton-Holt:
Ry=4hR0SSBySSB0(1−h)+SSBy(5h−1)exp(−0.5byσ2R+˜Ry)
Donde ˜Ry∼N(0,σ2R). R0 es el reclutamiento sin pesca, SSB0 es la biomasa desovante sin pesca, h es el steepness, by es el ajuste de sesgo aplicado durante el año y, σR es la desviación estándar de desviaciones de reclutamiento en el espacio log natural, y ˜Ry es es la desviación de reclutamiento lognormal.
Stock-reclutamiento
Usando la función Ricker:
Ry=R0SSBySSB0exp(h(1−SSBy/SSB0))exp(−0.5byσ2R+˜Ry)
Existen otras funciones stock-reclutamiento como: Hockey-Stick, Shepherd, Survivorship (Taylor et al. 2013), versión modificada de Ricker (Punt and Cope 2019).
Ajuste de sesgo
Aplicado para corregir sesgo entre transformaciones en escala natural y log (Methot and Taylor 2011). Normalmente se realiza un ajuste máximo durante el periodo con mayor cantidad de datos.
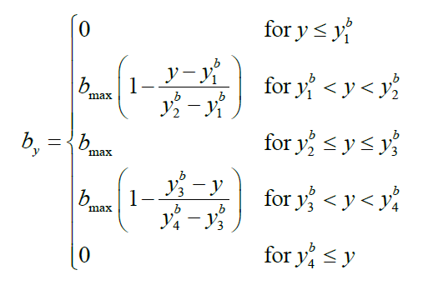
Ajuste de sesgo
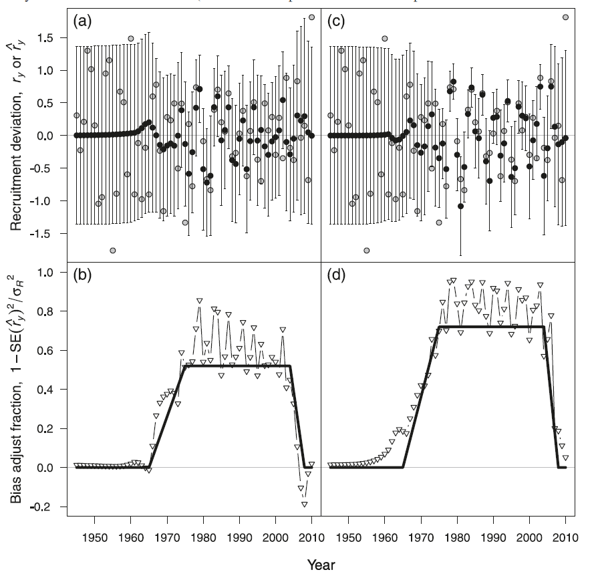
Methot and Taylor (2011)
Stock-reclutamiento
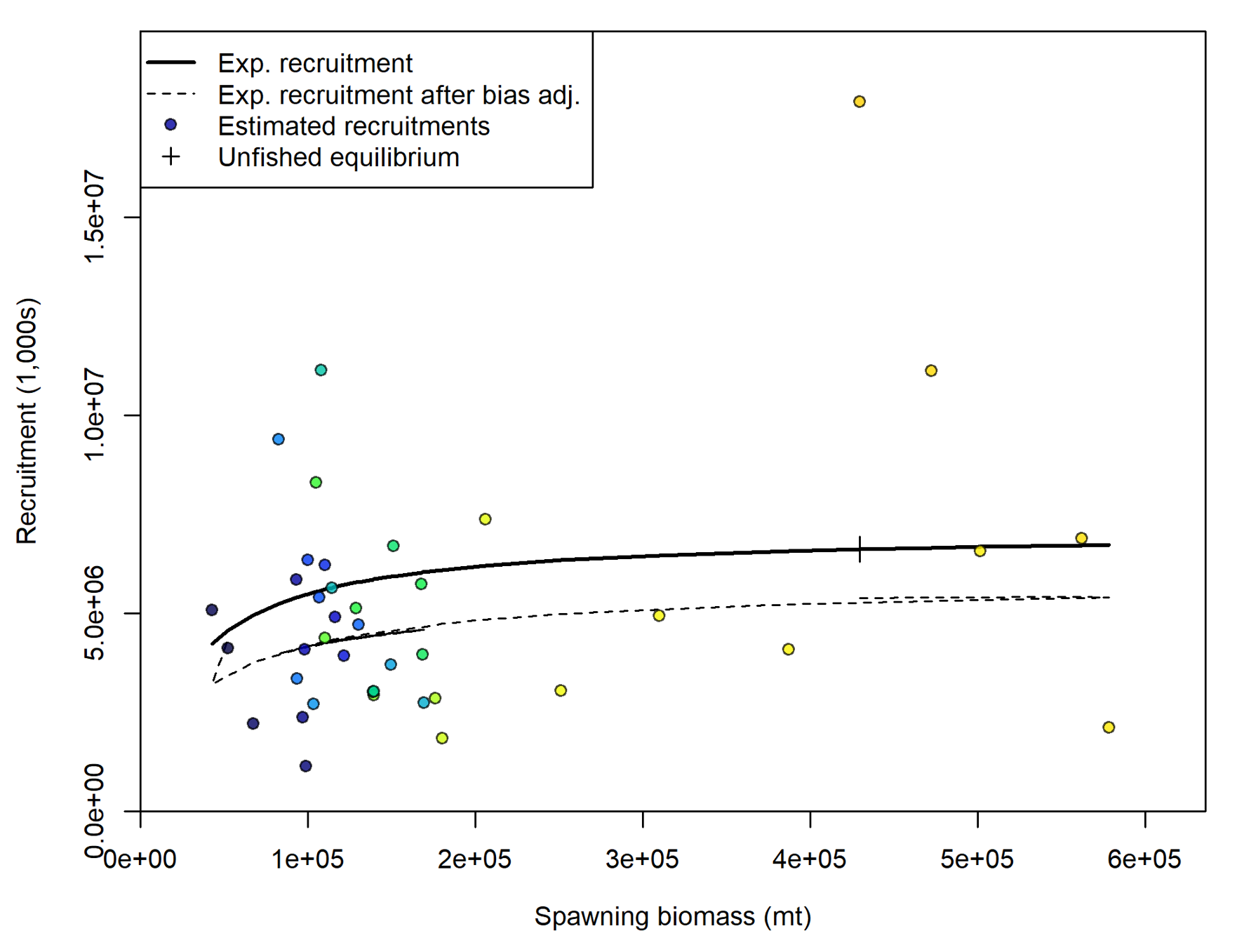
Reclutamiento
El desove ocurre una vez por año (configuración por defecto), pero varios eventos de reclutamiento pueden ser especificado dentro del año (settlements).
La propoción del reclutamiento anual en cada settlements es estimada como parámetros.
Referencias
