# Leer y escribir archivo de control: control.ss
control_file = SS_readctl(file = 'ss_models/simple/control.ss')
control_file$MG_parms
control_file$SR_parms
control_file$size_selex_types
# ... explorar
# Modificar el R object si es necesario
# Escribirlo nuevamente:
SS_writectl(ctllist = control_file, outfile = 'ss_models/simple/control.ss')Modelos avanzados en evaluación de recursos pesqueros
Dr. Giancarlo M. Correa
Cousteau Consultant Group
Modelo poblacional
Mortalidad natural
M es en muchos casos asumido constante para todas las edades (1 parámetro).
Hay opciones para especificar M específico a la edad, o que varíe en función a la talla:
- M independiente a la edad
- Lorenzen (Lorenzen 2022): toma en cuenta procesos fisiológicos a lo largo del ciclo de vida
- M específico a la edad relacionado a talla y madurez (Maunder et al. 2023)
Abundancia: estructura inicial
Calculamos la abundancia a la edad (a<A):
N0,a=R0exp(−aM)
Esta ecuación varía para el grupo plus A (ver Technical Description, Methot and Wetzel (2013)).
Abundancia: dinámica
Ny+1,a={Ry+1a=0Ny,a−1exp(−Zy,a)1≤a≤A−1Ny,A−1exp(−Zy,A−1)+Ny,Aexp(−Zy,A)a=A
Donde:
Zy,a=M+∑f(Sf,aFy,f)
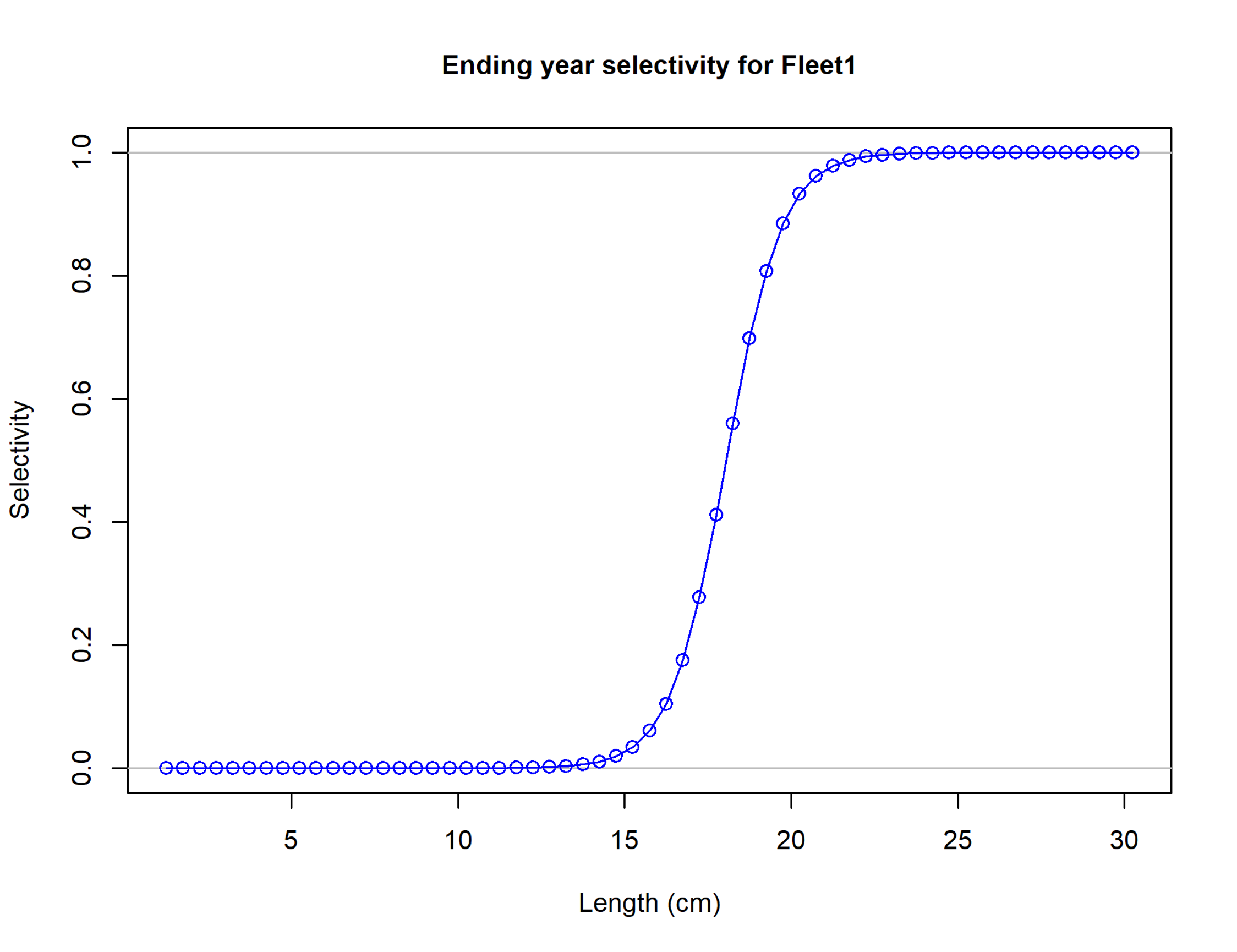
Selectividad
Se debe especificar selectividad a la edad y a la talla. La parametrización logística como función de talla es:
Sf,l=11+exp(−ln(19)(L′l−β1)/β2)
Donde β1 y β2 son parámetros.
Una de las parametrizaciones más utilizadas es la doble-normal (ver selectivity_options.R).
Selectividad
Captura
- Aproximación de Pope:
Ignoramos el subíndice de flota por simplicidad:
Ny+1,a+1=Ny,aexp(−M)−ˆCy,aexp(−M/2)
Luego, se puede aproximar F mediante:
Ny+1,a+1exp(M)=Ny,a−Ny,a(1−exp(−SaFy))
Ver Xiao and Wang (2007).
Captura
- Ecuación de captura de Baranov
Usamos:
ˆCy,a=SaFyM+SaFyNy,a(1−exp(−M−SaFy))
Donde Fy son parámetros estimados.
Captura
- Método híbrido: usa la ecuación de Pope y Baranov secuencialmente para estimar F.
- Aplica el método de Pope para obtener una tasa de cosecha en la season
- Conviente la tasa de cosecha al equivalente en la ecuación de Baranov Fhyb
- Ajusta valores Fhyb por medio de iteraciones usando el ratio de captura calculada y observada para cada flota
- Proceder con Fhyb en adelante.
Captura
- Método híbrido: combinación de métodos 2 y 3. Es el método recomendado ya que mejora algunos problemas existentes para el método 3 (e.g., altos valores de F, múltiples flotas).
Ejemplo de dinámica poblacional
Explorar el archivo Excel population-dynamics.xlsx.
Archivo de entrada: control.ss
control.ss
Línea de parámetro siempre tiene 14 valores:
| Columna | Elemento | Descripción |
|---|---|---|
| 1 | LO | Valor mínimo que puede tomar el parámetro |
| 2 | HI | Valor máximo que puede tomar el parámetro |
| 3 | INIT | Valor inicial del parámetro |
| 4 | PRIOR | Valor esperado del parámetro |
| 5 | PRIOR SD | Desviación estándar para el prior |
| 6 | PRIOR TYPE | Tipo de prior |
| 7 | PHASE | Fase de estimación |
control.ss
| Columna | Elemento | Descripción |
|---|---|---|
| 8 | Env var and Link | Enlace a serie de tiempo ambiental |
| 9 | Dev link | Uso de vector de desviación en la función de enlace |
| 10 | Dev min yr | Año inicial de desviación |
| 11 | Dev max yr | Año final de desviación |
| 12 | Dev phase | Fase para estimación de elementos en vector |
| 13 | Block | Bloque o tendencia a ser aplicado |
| 14 | Block function | Forma funcional para el bloque |
En algunas ocasiones (e.g., mortalidad por pesca), veremos que solo los primeros siete valores son necesarios (línea de parámetro corta).
control.ss
Explorar el archivo Excel
control-helper.xlsx(Ctl_Basicsheet) (obtenido de Stock Synthesis Virtual Lab).Explorar SS Manual (sección Control File).
Laboratorio
Preparación de archivo control
Preparar el archivo control para SS.
Podemos hacerlo en tres principales formas:
Modificando el archivo
control.ssdirectamente.Utilizando las funciones
SS_readctlySS_writectlder4ss.Utilizando el SS GUI (interfaz gráfica).
Preparación de archivo control
Ejemplo de cómo utilizar SS_readctl y SS_writectl.
Referencias
