Modelos avanzados en evaluación de recursos pesqueros

Dr. Giancarlo M. Correa

Cousteau Consultant Group

Modelo observacional

Composición por tallas y edades

Para obtener la composición por tallas y edades predicha para cada flota, SS primero calcula la captura a la talla y edad:

\[C_{y,f,a,l} = S_{f,l}S_{f,a}\varphi_{a,l}N_{y,a}exp(-\theta Z_{y,a})\]

Composición por tallas

Luego, la composición por talla predicha:

\[\hat{p}_{1,y,f,l}=\frac{\sum_a C_{y,f,a,l}+x}{\sum_l (\sum_a C_{y,f,a,l}+x)}\]

Donde \(x\) es una constante pequeña añadida (e.g., 1e-07).

Composición por edades

Para la composición de edades, primero tenemos que incluir el efecto de la matriz de error al estimar las edades de los individuos:

\[\psi_{a}=\begin{cases} \Phi(\frac{a_1 - \tilde{a}_a}{\tilde{a}_a})&a=1\\ \Phi(\frac{a_{a+1} - \tilde{a}_a}{\tilde{a}_a})-\Phi(\frac{a_a - \tilde{a}_a}{\tilde{a}_a})&1<a<A\\ 1-\Phi(\frac{A - \tilde{a}_a}{\tilde{a}_a})&a=A \end{cases}\]

Donde \(\tilde{a}_a\) es la edad esperada \(a\) en la mitad del año.

Composición por edades

Luego, la composición por edades predicha es calculada:

\[\hat{p}_{2,y,f,a}=\frac{\sum_l C_{y,f,a,l}+x}{\sum_a (\sum_l C_{y,f,a,l}+x)}\]

Índice de abundancia

Primero se calcula la biomasa vulnerable para la flota \(f\):

\[B^{vul}_{y,f} = \sum_l w_l \sum_a C_{y,f,a,l}\]

Luego, el índice predicho por el modelo (\(\hat{I}_{y,f}\)) es:

\[\hat{I}_{y,f} = Q_f B^{vul}_{y,f}\]

Además, existen otras relaciones no lineales posibles en SS.

Modelo estadístico

Función de verosimilitud global

Formado de la contribución de diferentes subcomponentes de verosimilitud:

\[L = \sum_i \sum_f \omega_{i,f}L_{i,f} + \omega_R L_R\]

Donde \(L\) es la función objetivo conjunta. \(i\) representa diferente fuente de datos, \(f\) es la flota, y \(L_{i,f}\) es la función objetivo de cada fuente de datos. \(L_R\) es la función objetivo del componente de reclutamiento. \(\omega\) es un factor de peso.

Capturas

La función objetivo para capturas es:

\[L_{1,f} = \sum_{y}\frac{(ln(C_{y,f})-ln(\hat{C}_{y,f}+x))^2}{2\sigma_{y,f}^2}\]

Donde \(\hat{C}_{y,f}\) es la captura observada.

Índice de abundancia

Para el caso de los índices, la función objetivo es:

\[L_{2,f} = \sum_y ln(CV_{y,f}\hat{I}_{y,f})+0.5(\frac{ln(I_{y,f}) - ln(\hat{I}_{y,f})}{CV_{y,f}\hat{I}_{y,f}})^2\]

Donde \(I_{y,f}\) representa el índice observado. Se asume una distribución lognormal del error, y la correción de sesgo ha sido omitida.

Composición por tallas

Normalmente asumimos una distribución de error multinomial. La función objetivo para este caso es:

\[L_{3,f} = \sum_y \sum_l n_{1,y,f} p_{1,y,f}ln(\frac{p_{1,y,f,l}}{\hat{p}_{1,y,f,l}})\]

Donde \(p_{1,y,f}\) es la composición por tallas observada y \(n_1\) representa el tamaño de muestra (\(Nsamp\)).

Composición por edades

Normalmente asumimos una distribución de error multinomial. La función objetivo para este caso es:

\[L_{4,f} = \sum_y \sum_a n_{2,y,f} p_{2,y,f}ln(\frac{p_{2,y,f,l}}{\hat{p}_{2,y,f,l}})\]

Donde \(p_{2,y,f}\) es la composición por edades observada y \(n_2\) representa el tamaño de muestra (\(Nsamp\)).

Reclutamiento

La función objetivo es:

\[L_R = 0.5(\sum_y \frac{\tilde{R}^2_y}{\sigma_R^2}+b_yln(\sigma_R^2))\]

Estimación de parámetros

Objetivo: reducir al mínimo posible la discrepancia entre los valores predichos del modelo y los datos.

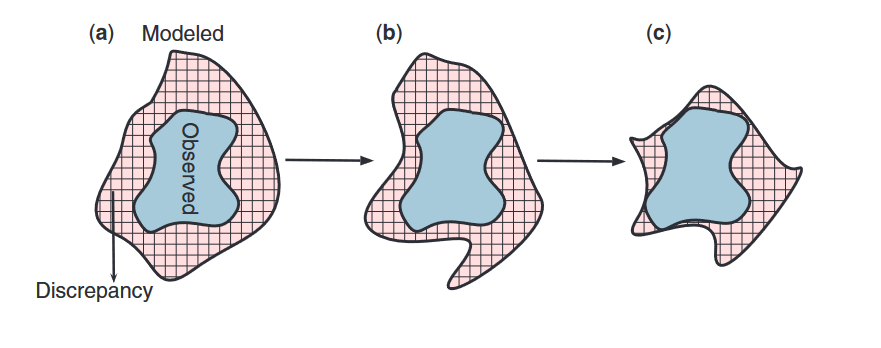
Subbey (2018)

Estimación de parámetros

Algoritmo de diferenciación automática (AD): basados en métodos de gradiente descendente. Generalmente son rápidos, estables y exactos.

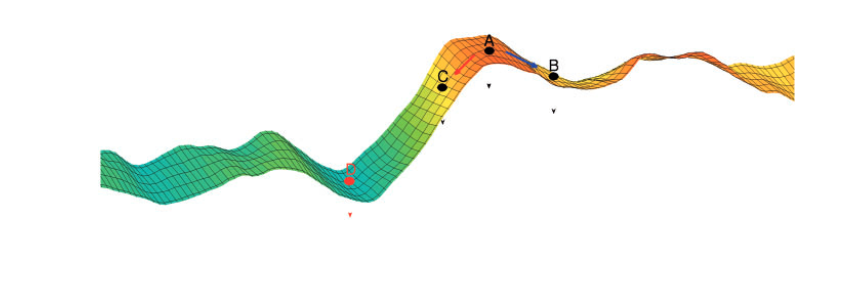
Subbey (2018)

Estimación de parámetros

Superficie puede llegar a ser muy compleja en modelos con muchos parámetros.

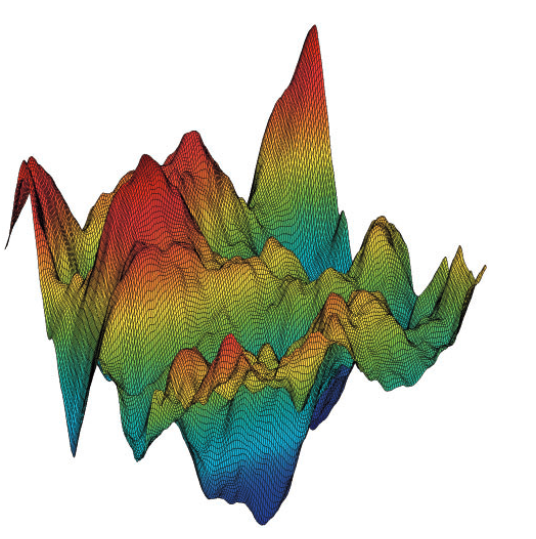
Subbey (2018)

Algoritmo AD

Deficiencia 1: La superficie no es única, depende del tipo de error asumido.

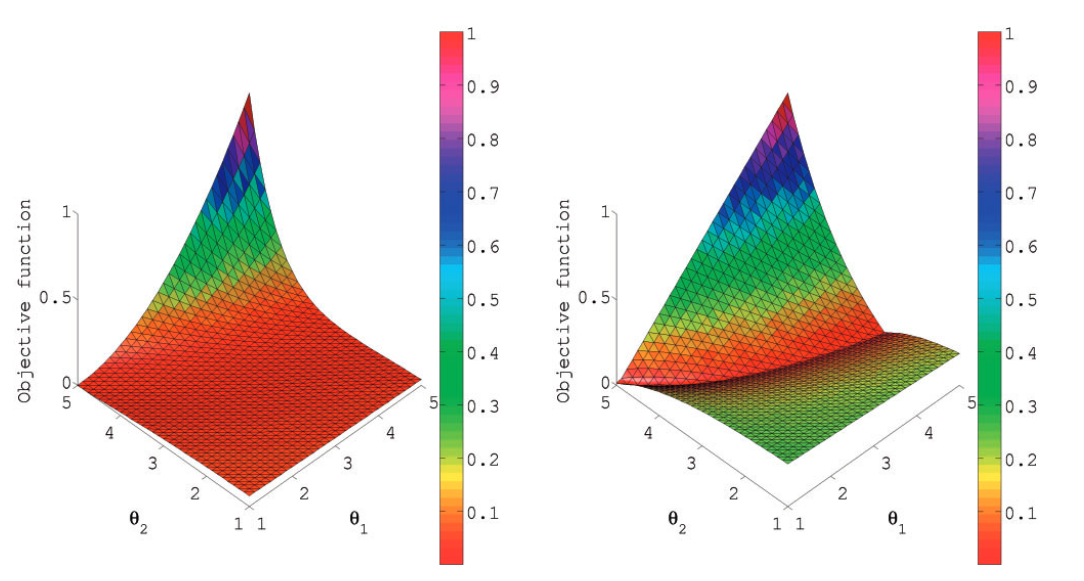
Subbey (2018)

Algoritmo AD

Deficiencia 2: Punto de partida (INIT) puede tener una gran influencia.

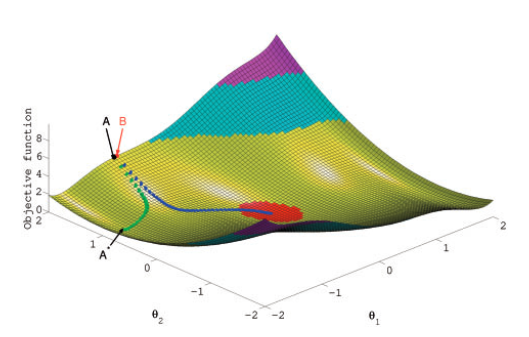
Subbey (2018)

Algoritmo AD

Deficiencia 3: Criterio de convergencia (especificado en starter.ss) no garantiza mínimo global.

Deficiencia 4: Falla en convergencia puede ser debido a parámetros del algoritmo.

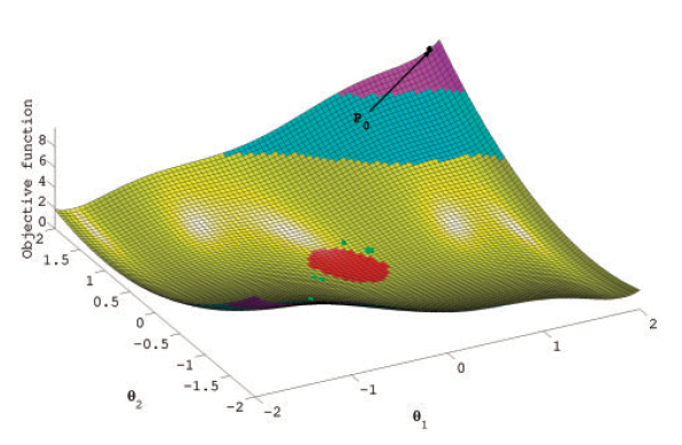
Model sculpting

Se centra en espeficiar límites a los parámetros (LO y HI) y fases de estimación (PHASE), con el objetivo que los parámetros no tomen valores irreales.

Fases de estimación

Ejemplo:

Fase 1: el algoritmo optimiza la función objetivo (\(L\)) estimando los parámetros en fase 1 (mantiene fijos los demás).
Fase 2: el algoritmo optimiza la función objetivo (\(L\)) estimando los parámetros en fase 1 y 2 (mantiene fijos los demás).
Fase 3: el algoritmo optimiza la función objetivo (\(L\)) estimando los parámetros en fase 1, 2, y 3 (mantiene fijos los demás).

Punt et al. (2013) recomienda estimar parámetros que escalan la biomasa (e.g. \(R_0\)) en primeras fases y selectividad en últimas fases.

Análisis de resultados

Report.sso

Los principales resultados estarán en Report.sso y podemos analizarlo directamente.

Una opción más eficiente es utilizando las funciones de r4ss:

# Leer archivo Report.sso en R:
my_model = SS_output(dir = 'ss_models/simple')
my_model$maximum_gradient_component # criterio de convergencia
my_model$parameters # parametros estimados
my_model$breakpoints_for_bias_adjustment_ramp # biad adj recomendado por SS
my_model$recruit # valores asociados con reclutamiento
my_model$timeseries # series de tiempo de biomasa, SSB, captura, etc
my_model$natage # abundancia a la edad
my_model$catage # abundancia a la edad
# ... explorar

Figuras

r4ss es recomendable para realizar figuras de salidas de modelos:

# Figuras:
SSplotBiology(my_model) # figuras de biologia
SSplotSelex(my_model) # figuras de selectividad
SSplotData(my_model) # datos de entrada
SSplotComps(my_model) # composicion por tallas y edad
# ... explorar

# Produce todas las figuras y las muestra en HTML:
SS_plots(my_model)

Diagnostico

Objetivo: verificar si el modelo se comporta adecuadamente y evaluar misspecification (Carvalho et al. 2021).

Existe un conjuto de diagnosticos desarrollados para modelos integrados. Para SS, examinar la librería en R ss3diags.

Introducción al manejo pesquero

Estado del stock

Los puntos de referencia más utilizados son los asociados a \(MSY\) (e.g., \(SSB_{MSY}\)) y estado sin pesca (e.g., \(SSB_0\)). Explorar las primeras líneas de forecast.ss para especificar la estimación de estos puntos de referencia.

Depletion es comunmente explorado para saber qué tanto la biomasa ha disminuido con respecto a un valor de referencia. Por ejemplo: \(SSB_y/SSB_0\).

Estado del stock

Kobe plot

Proyecciones

ICCAT

Proyecciones

Existen dos principales formar de realizar proyecciones en SS, las cuales se controlan desde forecast.ss:

Introducir valores de captura o F por flota para un periodo de proyección
Usar una regla de cosecha

Regla de cosecha

Pew Charitable Trusts

Evaluación de estrategia de manejo

Simula todo el proceso de manejo, y evalúa impactos de estrategias de manejo (Punt et al. 2014).

Bunnefeld et al. (2011)

Evaluación de estrategia de manejo

SS puede ser usado dentro de un proceso de evaluación de estrategia de manejo. Explorar la librería en R SSMSE (Doering and Vaughan 2024).

Referencias

Bunnefeld, N., Hoshino, E., and Milner-Gulland, E.J. 2011. Management strategy evaluation: A powerful tool for conservation? Trends in Ecology & Evolution 26: 441–447. Elsevier BV. doi:10.1016/j.tree.2011.05.003.

Carvalho, F., Winker, H., Courtney, D., Kapur, M., Kell, L., Cardinale, M., Schirripa, M., Kitakado, T., Yemane, D., Piner, K.R., Maunder, M.N., Taylor, I., Wetzel, C.R., Doering, K., Johnson, K.F., and Methot, R.D. 2021. A cookbook for using model diagnostics in integrated stock assessments. Fisheries Research 240: 105959. Elsevier BV. doi:10.1016/j.fishres.2021.105959.

Doering, K., and Vaughan, N. 2024. SSMSE: Management strategy evaluation (MSE) using stock synthesis (SS). Available from https://github.com/nmfs-fish-tools/SSMSE.

Punt, A.E., Butterworth, D.S., Moor, C.L. de, Oliveira, J.A.A.D., and Haddon, M. 2014. Management strategy evaluation: Best practices. Fish and Fisheries 17: 303–334. Wiley. doi:10.1111/faf.12104.

Punt, A.E., Huang, T., and Maunder, M.N. 2013. Review of integrated size-structured models for stock assessment of hard-to-age crustacean and mollusc species. ICES Journal of Marine Science 70: 16–33. Oxford University Press (OUP). doi:10.1093/icesjms/fss185.

Subbey, S. 2018. Parameter estimation in stock assessment modelling: Caveats with gradient-based algorithms. ICES Journal of Marine Science 75(5): 1553–1559. Oxford University Press (OUP). doi:10.1093/icesjms/fsy044.