Modelos avanzados en evaluación de recursos pesqueros: Día 1
Dr. Giancarlo M. Correa
Cousteau Consultant Group
Modelos estructurados por edad
Sistema pesquero
¿Para qué nos sirven los modelos de evaluación?

Conceptos básicos
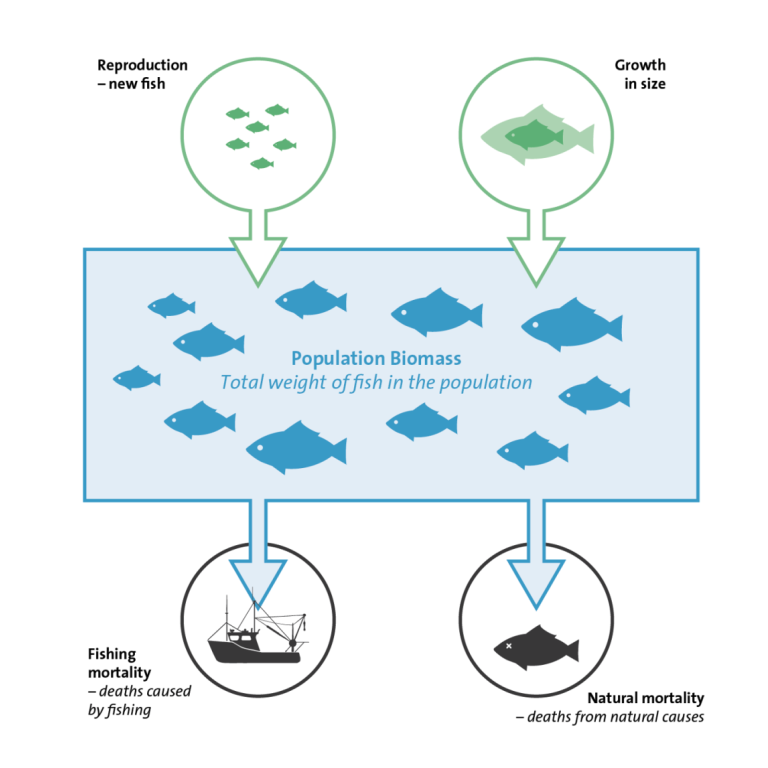
Stockholm University Baltic Sea Centre
Conceptos básicos
Diferencias claves en enfoques para estudiar poblaciones:
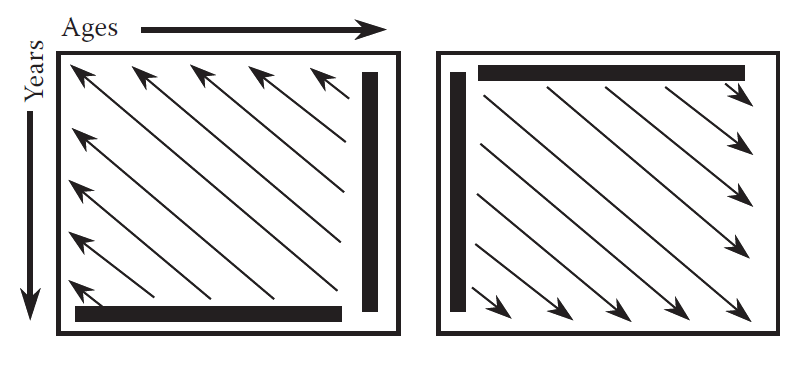
Haddon (2011)
Enfoque integrado
Combina diferentes tipos de datos en un único análisis. El ajuste a los datos se realiza por medio de una rutina de minimización de alguna función objetivo (D. Fournier and Archibald 1982).
Tipos de datos más comunes:
- Capturas
- Índices de abundancia
- Composición por tallas o edades
- Marcaje y recaptura
Enfoque integrado

Haddon (2011)
Conceptos básicos
En un modelo de evaluación estructurado por edades tenemos los siguientes componentes principalmente:
- Reclutamiento
- Mortalidad (natural y por pesca)
- Selectividad
- Crecimiento somático
Plataforma de evaluación
Software o librería orientado a la implementación de modelos de evaluación de stocks (en general).
Ventajas
- No hay necesidad de codificar
- Comunicación más sencilla
Desventajas
- No pueden ser aplicables a todos los stocks
- Efecto de caja negra
Plataforma de evaluación
Ejemplos:
- Stock Synthesis (Methot and Wetzel 2013)
- MULTIFAN-CL (Daid A. Fournier, Hampton, and Sibert 1998)
- SAM (Nielsen and Berg 2014)
- WHAM (Stock and Miller 2021)
Introducción a modelos state-space
Modelos state-space
Definición
- SSM permiten diferenciar y separar variaciones en procesos de un sistema de los errores de observación.
Podemos tener dos series temporales:
- Serie de procesos, o estados, que representan los cambios verdaderos en el sistema.
- Serie de observaciones que realizamos del sistema.
Los procesos cambian en el tiempo estocásticamente, lo que se conoce como variaciones en procesos (process variation).
Modelos state-space
- zt: estado en tiempo t (e.g., abundancia de la población)
- yt: observaciones
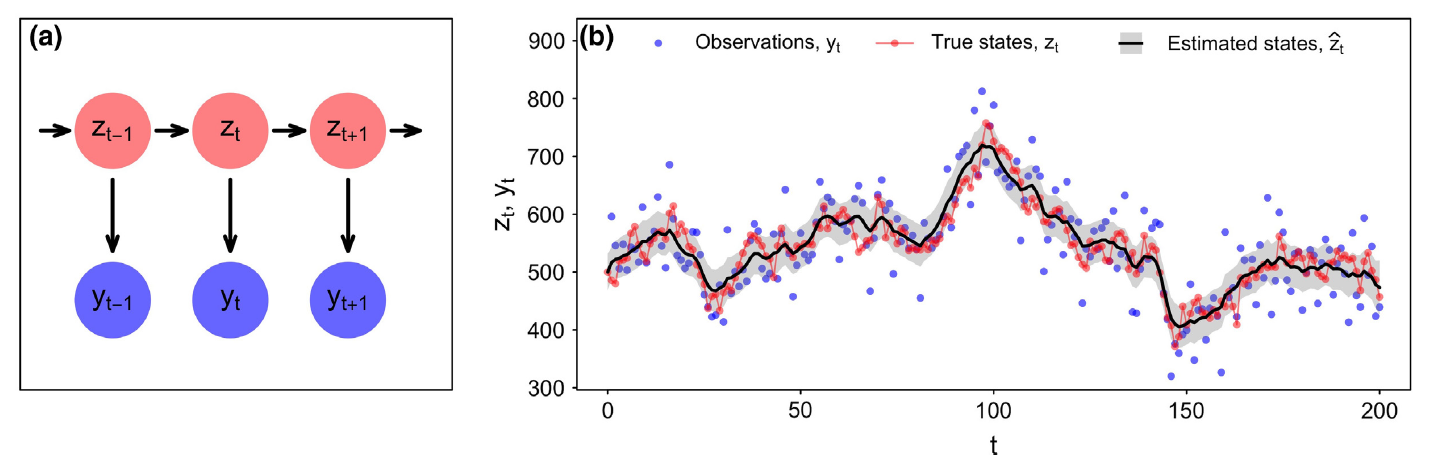
Auger-Méthé et al. (2021)
Modelos state-space
Normalmente se asume un proceso Markov (de primer orden) para modelar los estados:
zt=βzt−1+ϵt
- β: autocorrelación de estados en el tiempo
- ϵ: variación de procesos, donde:
ϵt∼N(0,σ2p)
z0 puede ser tratado como un parámetro adicional.
Modelos state-space
Para el caso de las observaciones, se asumen que estas son independientes, y se relacionan con los estados:
yt=αzt+ηt
- α: parámetro que regula el sesgo entre observación y estado
- η: error de observación, donde:
ηt∼N(0,σ2o)
Modelos state-space
Podemos caracterizar este modelo en términos de distribuciones de probabilidad:
g(yt∣zt,θo)
f(zt∣zt−1,θp)
para t=1,...,T, donde f y g son dos funciones de densidad de probabilidad normales, θp y θo son vectores de parámetros asociados con cada ecuación:
θp=(β,σ2p),θo=(α,σ2o)
Modelos state-space
Los efectos fijos vienen a ser:
θ=(θp,θo,z0)
Y los estados zt son tratados como variables aleatorias.
Por lo tanto, los SSM se consideran estos modelos jerárquicos:
- Primer nivel: ecuación de observación
- Segundo nivel: ecuación de proceso
Modelos state-space
- Aplicaciones a una gran variedad de campos de investigación.
- Enfoque utilizado para analizar series de tiempo en ecología:
- movimiento de animales
- biologging
- datos de captura-recaptura
- epidemiología
- evaluación de stocks
SSM en evaluación de stocks
Enfoque presentado por Sullivan (1992) y Gudmundsson (1994).
Usualmente los estados zt vienen a ser variables como (Aeberhard, Flemming, and Nielsen 2018):
- Abundancia a la edad
- Reclutamiento
- Mortalidad por pesca
- Mortalidad natural
- Selectividad
SSM en evaluación de stocks
En modelos de evaluación tradicionales se emplea el enfoque de máxima verosimilitud penalizada (PML) para modelar variaciones temporales en algún estado.
Ejemplo
Para modelar mortalidad por pesca, se separa la mortalidad por pesca anual y la selectividad a la edad:
Fa,t=ftSaexp(δa,t)
Asumiendo que δa,t∼N(0,σ2δ). El enfoque PML fija σ2δ (penalty term) en el modelo a un valor subjetivo.
Principal ventaja de SSM: estimación de σ2δ.
SSM en evaluación de stocks
En la actualidad, TMB (Kristensen et al. 2016) es la principal plataforma para implementar SSM debido a su eficiencia para modelar efectos aleatorios.
- Desarrollado a partir de ADMB (David A. Fournier et al. 2012)
- Usa la maquinaria de C++
- Sencilla manipulación desde R
Laboratorio
Software requerido
Instalación de librerías
Instalar TMB:
Para instalar WHAM, utilizaremos la versión que permite incluir datos de tallas:
También les sugiero explorar la versión base de WHAM.
Modelo sencillo en TMB
Objetivo: Conocer los pasos para implementar un modelo en TMB
Ejemplo obtenido de Sean Anderson (Gompertz SSM).
Modelo sencillo en TMB
- Tener en claro el sistema a modelar:
ut=a+but−1+ϵt yt=ln(ut)
ϵt∼N(0,σ2p) yt∼N(ln(ut),σ2o)
Donde ut es el estado (abundancia) en la población.
Modelo sencillo en TMB
- Implementar tu modelo en TMB (ver
Ejercicio_1.cpp)
// Header
#include <TMB.hpp>
template<class Type>
Type objective_function<Type>::operator() () {
// Input data:
DATA_VECTOR(y);
// Parameters (fixed and random variables):
PARAMETER(a);
PARAMETER(b);
PARAMETER(log_sigma_proc);
PARAMETER(log_sigma_obs);
PARAMETER_VECTOR(u);
// Transformed parameters if required
Type sigma_proc = exp(log_sigma_proc);
Type sigma_obs = exp(log_sigma_obs);
// Reports on transformed parameters:
ADREPORT(sigma_proc)
ADREPORT(sigma_obs)
int n = y.size(); // get time series length
Type nll = 0.0; // initialize negative log likelihood
// process model:
for(int i = 1; i < n; i++){
Type m = a + b * u[i - 1]; // Gompertz
nll -= dnorm(u[i], m, sigma_proc, true); // nll function
}
// observation model:
for(int i = 0; i < n; i++){
nll -= dnorm(y[i], u[i], sigma_obs, true); // nll function
}
return nll;
}Modelo sencillo en TMB
- Implementar tu modelo en TMB (ver
Ejercicio_1.cpp)
// Header
#include <TMB.hpp>
template<class Type>
Type objective_function<Type>::operator() () {
// Input data:
DATA_VECTOR(y);
// Parameters (fixed and random variables):
PARAMETER(a);
PARAMETER(b);
PARAMETER(log_sigma_proc);
PARAMETER(log_sigma_obs);
PARAMETER_VECTOR(u);
// Transformed parameters if required
Type sigma_proc = exp(log_sigma_proc);
Type sigma_obs = exp(log_sigma_obs);
// Reports on transformed parameters:
ADREPORT(sigma_proc)
ADREPORT(sigma_obs)
int n = y.size(); // get time series length
Type nll = 0.0; // initialize negative log likelihood
// process model:
for(int i = 1; i < n; i++){
Type m = a + b * u[i - 1]; // Gompertz
nll -= dnorm(u[i], m, sigma_proc, true); // nll function
}
// observation model:
for(int i = 0; i < n; i++){
nll -= dnorm(y[i], u[i], sigma_obs, true); // nll function
}
return nll;
}Modelo sencillo en TMB
- Implementar tu modelo en TMB (ver
Ejercicio_1.cpp)
// Header
#include <TMB.hpp>
template<class Type>
Type objective_function<Type>::operator() () {
// Input data:
DATA_VECTOR(y);
// Parameters (fixed and random variables):
PARAMETER(a);
PARAMETER(b);
PARAMETER(log_sigma_proc);
PARAMETER(log_sigma_obs);
PARAMETER_VECTOR(u);
// Transformed parameters if required
Type sigma_proc = exp(log_sigma_proc);
Type sigma_obs = exp(log_sigma_obs);
// Reports on transformed parameters:
ADREPORT(sigma_proc)
ADREPORT(sigma_obs)
int n = y.size(); // get time series length
Type nll = 0.0; // initialize negative log likelihood
// process model:
for(int i = 1; i < n; i++){
Type m = a + b * u[i - 1]; // Gompertz
nll -= dnorm(u[i], m, sigma_proc, true); // nll function
}
// observation model:
for(int i = 0; i < n; i++){
nll -= dnorm(y[i], u[i], sigma_obs, true); // nll function
}
return nll;
}Modelo sencillo en TMB
- Compilar el modelo (en R):
Modelo sencillo en TMB
- En R, leer tus datos. Imaginemos que
yson tus observaciones:
[1] 3.857919 4.139282 4.166160 4.593082 4.487591 4.691392 4.876311 4.681899
[9] 4.581784 4.706909 4.361975 4.900340 4.493509 4.841002 4.922498 4.722094
[17] 5.041822 4.885910 4.346571 4.497004 4.620252 4.214646 4.341192 4.251093
[25] 4.634612 4.130690 4.092495 4.414942 4.317848 4.315265 4.970341 4.852596
[33] 4.682839 4.766740 4.560845 5.270630 4.776654 5.206920 5.310690 4.500237
[41] 4.816574 4.481971 4.218075 4.016740 4.537255 4.935705 4.412348 4.750295
[49] 4.955589 4.473484 4.852497 4.890937 4.776721 4.486947 4.931865 4.767796
[57] 5.192605 4.571766 4.964695 4.688365 4.988027 4.610332 4.421622 5.253123
[65] 4.336354 4.339095 4.583634 4.512310 4.740320 4.904109 5.148162 4.948719
[73] 4.386315 5.102028 4.383329 4.215316 4.716833 4.701634 4.490838 4.427061
[81] 4.322670 4.828525 4.610247 4.428890 4.703014 4.641656 4.965105 4.956500
[89] 5.095534 4.696261 5.029934 5.024695 5.091339 4.819369 4.511168 5.412903
[97] 4.909512 4.939771 5.217307 4.853442Modelo sencillo en TMB
- Preparar los objetos y correr el modelo:
# Data input (list)
data <- list(y = y)
# fixed effects and random variables (list):
parameters <- list(a = 1, b = 0.5, log_sigma_proc = -1,
log_sigma_obs = -1, u = rep(mean(y), 100))
# Construct objective function (define random variable):
obj <- MakeADFun(data, parameters, random = "u", DLL = "Ejercicio_1")
obj$hessian <- FALSE # no calculate hessian
# Optimization:
opt <- nlminb(start = obj$par, obj = obj$fn, gr = obj$gr)
# Calculate SD of model parameters
est_pars <- sdreport(obj)Modelo básico de evaluación de stocks
Abrir archivo Ejercicio_2.xlsx
Referencias
