Modelos avanzados en evaluación de recursos pesqueros: Día 2


Dr. Giancarlo M. Correa


Cousteau Consultant Group

The Woods Hole Assessment Model (WHAM)

WHAM: Introducción


WHAM: Introducción


  • Antes de Stock and Miller (2021), varios estudios ya habían ido publicando los inicios de WHAM:
    • Stock et al. (2021)
    • Miller, O’Brien, and Fratantoni (2018)
    • Miller and Hyun (2018)
    • Miller, Hare, and Alade (2016)

WHAM: Requerimientos

Se require lo siguiente:

  • Disponibilidad de datos y conocimiento del stock.
  • Solo se usa R para la implementación de un modelo.
  • Se recomienda conocimiento básico en TMB.
  • Conocimiento de las ecuaciones de dinámica poblacional en WHAM.

Recomendación

Si solo se tienen datos de captura e índices de abundancia, se recomienda usar otras plataformas, por ejemplo: SPiCT (Pedersen and Berg 2016), REMA.

WHAM: Datos

Con la nueva extensión de WHAM (Correa et al. 2023), podemos incluir los siguientes tipos de datos por año y flota (pesquerías e índices):

  • Captura total (solo para pesquerías)
  • Índices de abundancia (solo para índices)
  • Composición por edades y tallas
  • Conditional age-at-length (CAAL)
  • Variables ambientales
  • Matrix de error de edad
  • Peso medio a la edad

WHAM: Secciones

Modelamiento de las siguientes secciones de la dinámica poblacional del stock:

  • Reclutamiento (abundancia a la edad)
  • Selectividad
  • Mortalidad natural
  • Capturabilidad
  • Variables ambientales
  • Crecimiento somático

WHAM: Implementar un modelo

  1. Crear una lista en R con los datos de entrada:


input_data = list()
input_data$ages # Vector con edades 
input_data$catch_paa # Matrix con determinadas dimensiones 
input_data$index_paa # Matrix con determinadas dimensiones
# Y asi para capturas, composición de tallas, etc.

WHAM: Implementar un modelo

  1. Crear una lista en R con los datos de entrada:

Importante

  • La palabra catch ó fleet se refiere a las pesquerías y index a los índices (e.g., cruceros).
  • No es necesario especificar todos los slots. Si algún slot no es especificado, este tomará el valor por defecto.
  • Las dimensiones son estrictas (no mucha flexibilidad).
  • Los datos de entrada también puede ser especificado a partir de un archivo ASAP3.

WHAM: Implementar un modelo

  1. Crear el objeto de entrada para WHAM:
my_input = wham::prepare_wham_input(model_name = "Example_1",
                         basic_info = input_data, 
                         NAA_re = list(), # Recruitment parameters
                         M = list(), # M parameter
                         selectivity = list(), # Selectivity parameter
                         catchability = list(), # Catchability parameter
                         ecov = list(), # Environmental information
                         # Crecimiento somatico:
                         growth = list(), LAA = list(), # Mean length-at-age
                         LW = list(), # Length-weight relationship
                         WAA = list(), # Mean weight-at-age
                         age_comp = "multinomial", # Age composition model
                         len_comp = "multinomial" # Length composition model
                         )

WHAM: Pasos para implementar un modelo

  1. Crear el objeto de entrada para WHAM:

Importante

  • Al igual que para los datos de entrada, no necesitamos especificar todos los argumentos de prepare_wham_input. Si un argumento no es especificado, tomará el valor por defecto.
  • En el slide anterior, en el list() de cada argumento especificamos la información de cada parámetro.

WHAM: Implementar un modelo


Veremos que my_input tiene 4 principales slots:

my_input$data # datos
my_input$par # informacion de parametros
my_input$map # estimar/no estimar parametros
my_input$random # variables aleatorias


  1. Opcional: Fijar algunos parámetros
# Por ejemplo, podemos fijar sigma R:
my_input$map$log_NAA_sigma = factor(NA)

WHAM: Implementar un modelo


  1. Correr el modelo
my_model = wham::fit_wham(my_input)


  1. Analizar resultados
wham::plot_wham_output(my_model)

Datos de entrada

Información básica


input_data = list()
input_data$ages = 1:10 # edades
input_data$lengths = seq(from = 2, to = 120, by = 2) # tallas
input_data$years = 1971:2020 # years
input_data$n_fleets = 1 # numero de pesquerias
input_data$n_indices = 1 # numero de indices

Información de pesquería


Primero calculemos el número de años, edades, y tallas para hacer el resto más sencillo:

n_years = length(input_data$years)
n_ages = length(input_data$ages)
n_lengths = length(input_data$lengths)

Información de pesquería

# Captura agregada:
input_data$agg_catch = matrix(mis_datos, ncol = input_data$n_fleets, nrow = n_years) # Obs
input_data$catch_cv = matrix(mis_datos, ncol = input_data$n_fleets, nrow = n_years) # Obs error
# Composicion por edades (proporcion)
input_data$catch_paa = array(mis_datos, dim = c(input_data$n_fleets, n_years, n_ages)) # Obs
input_data$catch_Neff = matrix(mis_datos, ncol = input_data$n_fleets, nrow = n_years) # Obs error
# Composicion por tallas (proporcion)
input_data$catch_pal = array(mis_datos, dim = c(input_data$n_fleets, n_years, n_lengths)) # Obs
input_data$catch_NeffL = matrix(mis_datos, ncol = input_data$n_fleets, nrow = n_years) # Obs error
# Conditional age-at-length (CAAL, proporcion)
input_data$catch_caal = array(mis_datos, dim = c(input_data$n_fleets, n_years, n_lengths, n_ages)) # Obs
input_data$catch_caal_Neff = array(mis_datos, dim = c(n_years, input_data$n_fleets, n_lengths)) # Obs error
# Aging error matrix
input_data$catch_aging_error = array(mis_datos, dim = c(input_data$n_fleets, n_ages, n_ages))

Cuidado

No es posible tener captura agregada igual a 0, se sugiere especificar un número pequeño.

Muestreo

Para un viaje de pesca o un lance de un crucero de investigación:

Muestreo

Después de muestrear muchos viajes de pesca o lances en un crucero, se suele construir una clave talla-edad (probabilidad de ser cierta edad dada la talla):

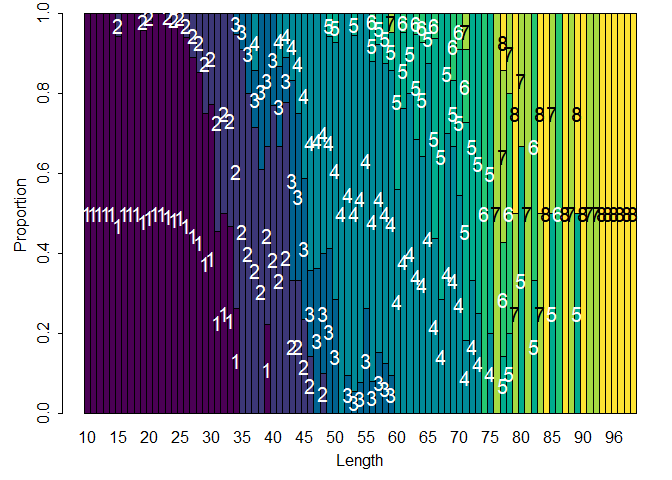
Muestreo

Finalmente, con los datos de la clave talla-edad y composición por talla por viaje o lance, se calcula la composición por edades por viaje o lance. Luego se realiza una expansión para todo el crucero o temporada de pesca.

Conditional age-at-length (CAAL)

CAAL es justamente la información talla-edad (clave talla edad).

El esfuerzo de muestreo se representa con Neff. Por ejemplo: número de viajes muestreados, o el no. de individuos muestreados por talla (del submuestreo de edades).

Información de índices

# Indice agregado:
input_data$agg_indices = matrix(mis_datos, ncol = input_data$n_indices, nrow = n_years) # Obs
input_data$index_cv = matrix(mis_datos, ncol = input_data$n_indices, nrow = n_years) # Obs error
# Información adicional:
input_data$units_indices = matrix(0L, nrow = n_years, ncol = input_data$n_indices) # 0 = numbers, 1 = biomass
input_data$fracyr_indices = matrix(0.5, ncol = input_data$n_indices, nrow = n_years) # fraccion del year
# Composicion por edades (proporcion)
input_data$index_paa = array(mis_datos, dim = c(input_data$n_indices, n_years, n_ages)) # Obs
input_data$index_Neff = matrix(mis_datos, ncol = input_data$n_indices, nrow = n_years) # Obs error
# Composicion por tallas (proporcion)
input_data$index_pal = array(mis_datos, dim = c(input_data$n_indices, n_years, n_lengths)) # Obs
input_data$index_NeffL = matrix(mis_datos, ncol = input_data$n_indices, nrow = n_years) # Obs error
# Conditional age-at-length (CAAL, proporcion)
input_data$index_caal = array(mis_datos, dim = c(input_data$n_indices, n_years, n_lengths, n_ages)) # Obs
input_data$index_caal_Neff = array(mis_datos, dim = c(n_years, input_data$n_indices, n_lengths)) # Obs error
# Aging error matrix
input_data$index_aging_error = array(mis_datos, dim = c(input_data$n_indices, n_ages, n_ages))

Selectividad pointers


Tenemos que especificar los pointers para los modelos de selectividad:

input_data$selblock_pointer_fleets = matrix(my_pointers, ncol = input_data$n_fleets, nrow = n_years)
input_data$selblock_pointer_indices = matrix(my_pointers, ncol = input_data$n_indices, nrow = n_years)


En palabras sencillas, es un tipo de indexación para saber que modelo de selectividad usará, por ejemplo, la pesquería 1, 2, 3, y el índice 1, 2 (ver sección de parámetros).

Peso a la edad

Puede ser tratado como empirical weight-at-age (asumimos que no tiene error) o como observaciones (error de observación asociado, waa_cv):

input_data$waa = array(mis_datos, dim = c(n_waa, n_years, n_ages))
input_data$waa_pointer_fleets = my_pointer_1 #length = n_fleets. 
input_data$waa_pointer_indices = my_pointer_2 #length = n_indices. 
input_data$waa_pointer_totcatch = my_pointer_3 #length = 1 
input_data$waa_pointer_ssb = my_pointer_4 #length = 1 
input_data$waa_pointer_jan1 = my_pointer_5 #length = 1 
input_data$waa_cv = array(mis_datos, dim = c(n_waa, n_years, n_ages)) # obs error

Los my_pointer, al igual que para selectividad, es una forma de indexación (indica la matrix de peso a la edad va a usar cierta pesquería o índice).

Activar datos


# Para pesquerias
input_data$use_agg_catch = matrix(mi_activar, nrow = n_years, ncol = input_data$n_fleets) # 1 = usar, 0 = no usar
input_data$use_catch_paa = matrix(mi_activar, nrow = n_years, ncol = input_data$n_fleets) # 1 = usar, 0 = no usar
input_data$use_catch_pal = matrix(mi_activar, nrow = n_years, ncol = input_data$n_fleets) # 1 = usar, 0 = no usar
input_data$use_catch_caal = array(mi_activar, dim = c(n_years, input_data$n_fleets, n_lengths)) # 1 = usar, 0 = no usar
input_data$use_catch_waa = matrix(mi_activar, nrow = n_years, ncol = input_data$n_fleets) # 1 = usar, 0 = no usar
input_data$use_catch_aging_error = rep(1, times = input_data$n_fleets) # 1 = si usar, 0 = no usar
# Para indices
input_data$use_indices = matrix(mi_activar, nrow = n_years, ncol = input_data$n_indices) # 1 = usar, 0 = no usar
input_data$use_index_paa = matrix(mi_activar, nrow = n_years, ncol = input_data$n_indices) # 1 = usar, 0 = no usar
input_data$use_index_pal = matrix(mi_activar, nrow = n_years, ncol = input_data$n_indices) # 1 = usar, 0 = no usar
input_data$use_index_caal = array(mi_activar, dim = c(n_years, input_data$n_indices, n_lengths)) # 1 = usar, 0 = no usar
input_data$use_index_waa = matrix(mi_activar, nrow = n_years, ncol = input_data$n_indices) # 1 = usar, 0 = no usar
input_data$use_index_aging_error = rep(1, times = input_data$n_indices) # 1 = si usar, 0 = no usar

Activar datos

Cuidado

Si no se incluyen datos de pal o caal, entonces el use será 0 automáticamente. Sin embargo, para paa, use es igual a 1 (activo) incluso si no incluimos datos de composición por edad. Por lo tanto, si no se desea usar datos de paa, especificar explicitamente use_paa igual a 0 en la matriz correspondiente.

Cuidado

Cuando se incluye datos de pal o caal o waa, también debemos especificar explicitamente el use igual a 1 en la matriz correspondiente.

Información adicional


input_data$maturity = matrix(mis_datos, nrow = n_years, ncol = n_ages) # madurez sexual
input_data$fracyr_SSB = matrix(mis_datos, ncol = 1, nrow = n_years) # fraction of year SSB
input_data$Fbar_ages = mis_datos # edades para calcular Fbar
input_data$percentSPR = 40 # % SPR reference point
input_data$percentFMSY = 100 # percent of FMSY to use for calculating catch in projections
input_data$simulate_period = c(1,0) # simulation for 1: model period, 2: projection
input_data$bias_correct_process = 1 # do process bias correction, 0 = no, 1 = yes
input_data$bias_correct_observation = 1 # do obs bias correction, 0 = no, 1 = yes

Referencias

Correa, Giancarlo M, Cole C Monnahan, Jane Y Sullivan, James T Thorson, and André E Punt. 2023. “Modelling Time-Varying Growth in State-Space Stock Assessments.” ICES Journal of Marine Science 80 (7): 2036–49. https://doi.org/10.1093/icesjms/fsad133.
Miller, Timothy J., Jonathan A. Hare, and Larry A. Alade. 2016. “A State-Space Approach to Incorporating Environmental Effects on Recruitment in an Age-Structured Assessment Model with an Application to Southern New England Yellowtail Flounder.” Canadian Journal of Fisheries and Aquatic Sciences 73 (8): 1261–70. https://doi.org/10.1139/cjfas-2015-0339.
Miller, Timothy J., and Saang-Yoon Hyun. 2018. “Evaluating Evidence for Alternative Natural Mortality and Process Error Assumptions Using a State-Space, Age-Structured Assessment Model.” Canadian Journal of Fisheries and Aquatic Sciences 75 (5): 691–703. https://doi.org/10.1139/cjfas-2017-0035.
Miller, Timothy J., Loretta O’Brien, and Paula S. Fratantoni. 2018. “Temporal and Environmental Variation in Growth and Maturity and Effects on Management Reference Points of Georges Bank Atlantic Cod.” Canadian Journal of Fisheries and Aquatic Sciences 75 (12): 2159–71. https://doi.org/10.1139/cjfas-2017-0124.
Pedersen, Martin W, and Casper W Berg. 2016. “A Stochastic Surplus Production Model in Continuous Time.” Fish and Fisheries 18 (2): 226–43. https://doi.org/10.1111/faf.12174.
Stock, Brian C., and Timothy J. Miller. 2021. “The Woods Hole Assessment Model (WHAM): A General State-Space Assessment Framework That Incorporates Time- and Age-Varying Processes via Random Effects and Links to Environmental Covariates.” Fisheries Research 240 (August): 105967. https://doi.org/10.1016/j.fishres.2021.105967.
Stock, Brian C., Haikun Xu, Timothy J. Miller, James T. Thorson, and Janet A. Nye. 2021. “Implementing Two-Dimensional Autocorrelation in Either Survival or Natural Mortality Improves a State-Space Assessment Model for Southern New England-Mid Atlantic Yellowtail Flounder.” Fisheries Research 237 (May): 105873. https://doi.org/10.1016/j.fishres.2021.105873.