Modelos avanzados en evaluación de recursos pesqueros: Día 6

Dr. Giancarlo M. Correa

Cousteau Consultant Group

WHAM: Valores esperados

Introducción

• Nos referimos a cantidades que el modelo predice y son contrastadas con observaciones. Por ejemplo: captura agregada predicha vs. captura agregada observada.
• Ya hemos ido viendo algunas variables:
  • Abundancia a la edad
  • Talla media a la edad
  • Peso medio a la edad

Captura a la edad y talla

Se calcula usando (Correa et al. 2023):

\[\hat{C}_{y,f,l,a} = \varphi_{y,l,a}S_{y,f,l}S_{y,f,a}F_{y,f}*N_{y,a}\frac{1-exp(-Z_{y,a})}{Z_{y,a}}\]

Donde \(f\) representa las pesquerías y \(Z_{y,a}\) es calculando usando \(F\) acumulado (para diferentes pesquerías).

Composición por talla y edades

Primero calculamos la sumatoria a lo largo de edades o tallas:

\[\hat{C}_{y,f,a} = \sum_l{\hat{C}_{y,f,l,a}}\hspace{2cm}\hat{C}_{y,f,l} = \sum_a{\hat{C}_{y,f,l,a}}\]

Luego, para calcular la composición marginal (proporción):

\[\hat{p}_{y,f,a}=\frac{\hat{C}_{y,f,a}}{\sum_{a}\hat{C}_{y,f,a}}\hspace{2cm}\hat{p}_{y,f,l}=\frac{\hat{C}_{y,f,l}}{\sum_{l}\hat{C}_{y,f,l}}\]

Captura agregada

Lo calculamos:

\[\hat{C}_{y,f}=\sum_a W_{y,a}\hat{C}_{y,f,a}\]

Donde \(W_{y,a}\) son los datos de peso a la edad que corresponde a la pesquería \(f\) (fracción del año).

Indice de abundancia

Se calcula usando:

\[\hat{I}_{y,i,l,a}=\varphi_{y,l,a}S_{y,i,l}S_{y,i,a}N_{a,y}exp(-f_{y,i}Z_{a,y})\]

Donde \(i\) indica el índice y \(f_{y,i}\) la fracción del año cuando el índice ocurre.

Indice de abundancia

Luego calculamos la sumatoria a lo largo de edades o tallas:

\[\hat{I}_{y,i,a} = \sum_l{\hat{I}_{y,i,l,a}}\hspace{2cm}\hat{I}_{y,i,l} = \sum_a{\hat{I}_{y,i,l,a}}\]

Luego, para calcular la composición marginal (proporción):

\[\hat{p}_{y,i,a}=\frac{\hat{I}_{y,i,a}}{\sum_{a}\hat{I}_{y,i,a}}\hspace{2cm}\hat{p}_{y,i,l}=\frac{\hat{I}_{y,i,l}}{\sum_{l}\hat{I}_{y,i,l}}\]

Indice de abundancia

Para el índice agregado (en peso):

\[\hat{I}_{y,i} = Q_{y,i}\sum_a W_{y,a}\hat{I}_{y,i,a}\]

Donde \(Q\) es la capturabilidad y \(W_{y,a}\) es el peso a la edad correspondiente a esa fracción del año.

Para el caso de índice agregado en abundancia, simplemente se omite \(W_{y,a}\).

WHAM: Aspectos estadísticos

Componentes de verosimilitud

1. Captura agregada:

Se asume una distribución normal de errores.

2. Indices de abundancia agregados:

Se asume una distribución normal de errores.

Componentes de verosimilitud

3. Peso a la edad:

Se asume una distribución normal de errores.

4. Variables ambientales:

Se asume una distribución normal de errores.

Componentes de verosimilitud

5. Composición a la edad y CAAL:

Tenemos varias opciones y lo podemos especificar:

my_input = prepare_wham_input(...,
                              age_comp = ..., # (character) Definir la distribucion de error
                              ...)

Se recomienda explorar Fisch et al. (2021).

Componentes de verosimilitud

• "multinomial": Opcion por defecto. 0 parámetros.
• "dir-mult": Dirichlet saturante. 1 parámetros.
• "dirichlet-pool0": Se agregan cantidades predecidas cuando hay ceros en observaciones (Francis 2014). 1 parámetro.
• "dirichlet-miss0": Trata los ceros en observaciones como valores faltantes. 1 parámetro.

Componentes de verosimilitud

• "logistic-normal-miss0": Logistic normal, trata valores ceros como faltantes (Francis 2014). 1 parámetro.
• "logistic-normal-ar1-miss0": Logistic normal, trata valores ceros como faltantes e incluye correlación temporal. 2 parámetros.
• "logistic-normal-pool0": Logistic normal, se hace la agregación como en dirichlet. 1 parámetros.

Componentes de verosimilitud

• "logistic-normal-01-infl": Cero o uno inflado logistic normal (Ospina and Ferrari 2012). 3 parámetros.
• "mvtweedie": Multivariate-tweedie (James T. Thorson, Miller, and Stock 2022). 2 parámetros.
• "dir-mult-linear": Linear Dirichlet multinomial (James T. Thorson et al. 2017). 1 parámetro.

Componentes de verosimilitud

Resumen (Francis 2014):

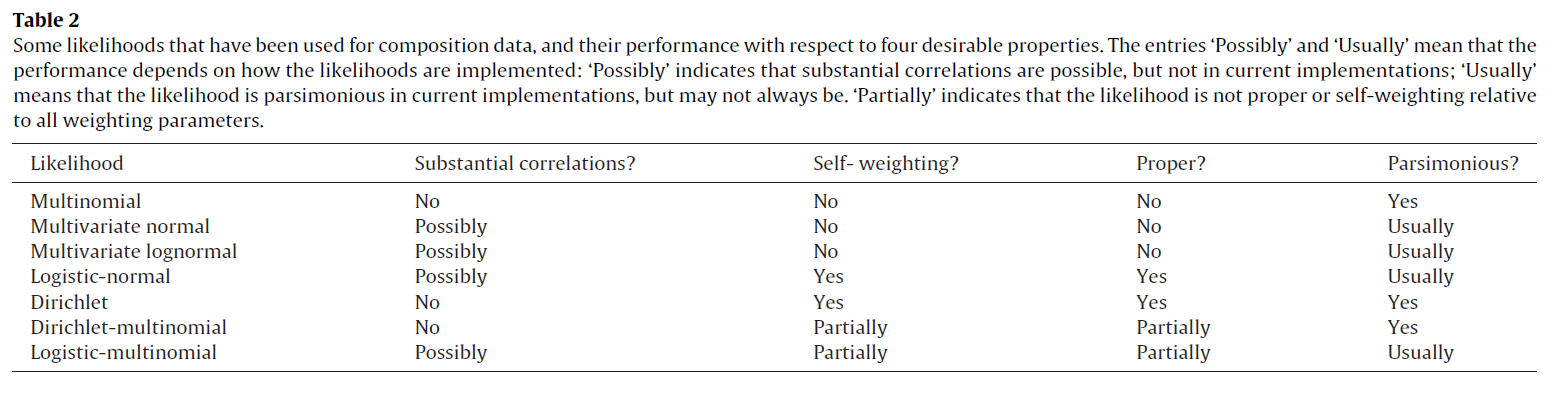
Componentes de verosimilitud

6. Composición a la talla:

Tenemos algunas opciones y lo podemos especificar:

my_input = prepare_wham_input(...,
                              len_comp = ..., # (character) Definir la distribucion de error
                              ...)

Componentes de verosimilitud

• "multinomial": Multinomial. 0 parámetros.
• "dir-mult": Dirichlet saturante. 1 parámetros.
• "dir-mult-linear": Linear Dirichlet multinomial (James T. Thorson et al. 2017). 1 parámetro.

Componentes de verosimilitud

No olvidar

Dado que WHAM puede ser catalogado como un modelo con enfoque integrado, todas estos componentes de verosimilitud son agregados en un solo componente, el cual será minimizado por el algoritmo de optimización.

WHAM: Aproximación de Laplace

Definición

El algoritmo de opmitización de TMB es el mismo que para ADMB. Ambas plataformas darán el mismo resultado para un mismo modelo.

Lo novedoso de TMB es que es mucho más rápido para modelos con efectos aleatorios (Kristensen et al. 2016).

Definición

‘Join likelihood’ función, la cual junta los componentes de observación y estados (todo el SSM) (Aeberhard, Flemming, and Nielsen 2018):

\[L_{joint}(\theta, y_{1:T},x_{0:t}) = p_\theta (x_0) \prod^T_{t=1} p_\theta (y_t \mid x_t)p_\theta (x_t \mid x_{t-1})\]

Sin embargo, lo visto anteriormente no es práctico. Por lo tanto, en ciencias pesqueras se suele utilizar dos enfoques para esto: frecuentista y bayesiano.

Enfoque frecuentista

Marginal likelihood:

\[L_{marginal}(\theta , y_{1:T}) = \int L_{joint}(\theta, y_{1:T}, x_{0:T})dx_{1:T}\]

Luego de integrar, the maximum likelihood estimator (MLE) para \(\theta\):

\[\hat{\theta}_{ML} = \arg \max_{\theta \in \Theta} logL_{marginal}(\theta,y_{1:T})\]

Enfoque frecuentista

Ahora, se necesitará alguna forma para integrar (o aproximar) el marginal likelihood. Es justamente aquí donde se utiliza la aproximación de Laplace, realizado de una manera eficiente en TMB.

Característica importante:

• El marginal likelihood debe ser cercano a una función unimodal (para ser aproximada mediante una función de densidad normal).

WHAM: Optimización

Overview

Objetivo: reducir las discrepancias.

(Subbey 2018)

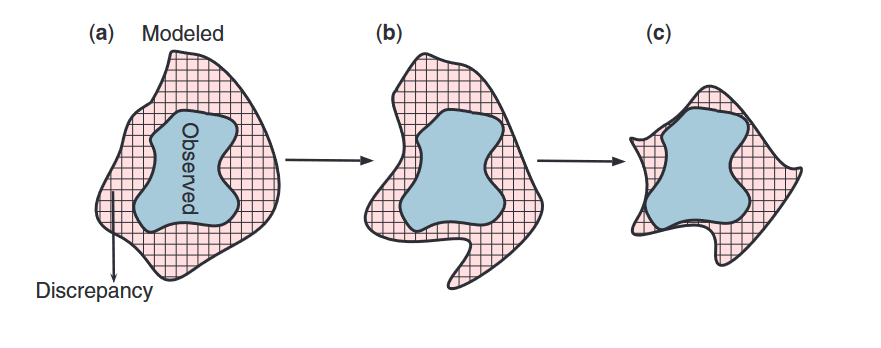
Gradient descent

¿Cómo?: Encontrar el mínimo:

(Subbey 2018)

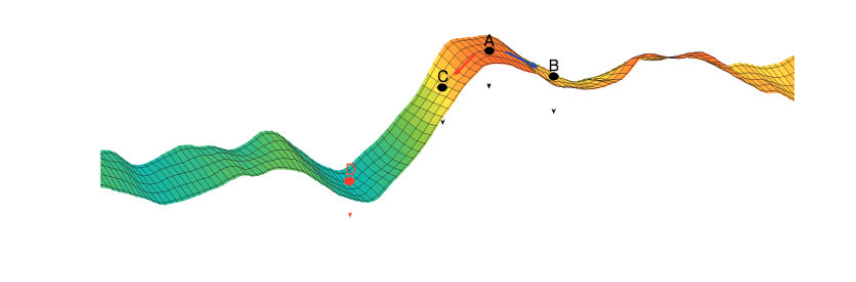
Gradient descent

Pero no es tan sencillo:

(Subbey 2018)

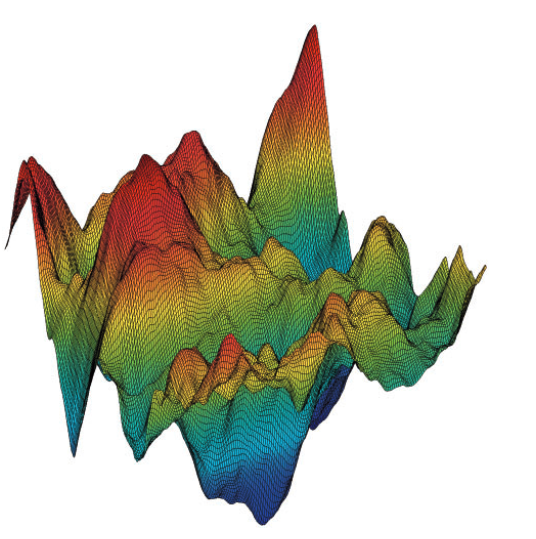
Gradient descent

Superficie depende de varios factores:

(Subbey 2018)

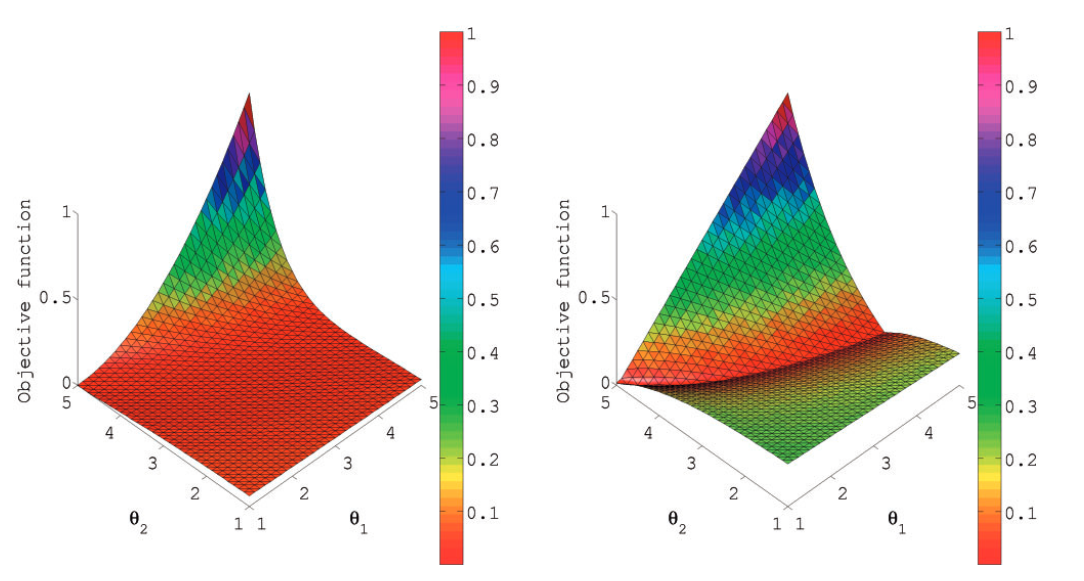
Gradient descent

Mínimo difícil de encontrar por diversos motivos:

(Subbey 2018)

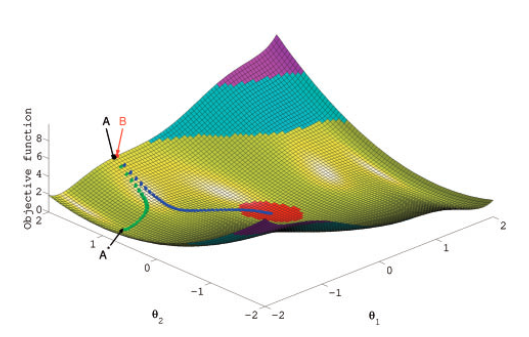
WHAM: One-step ahead (OSA) residuals

Definición

Usualmente para analizar datos de composición utilizamos los Pearson residuals. Sin embargo, cuando tenemos este tipo de datos, las observaciones no son independientes y pueden verse distribuidas diferente a la normal.

Los OSA residuals aparecen para lidiar con este problema, los cuales de-correlacionan datos de composición cuando estimamos residuos estandarizados (Trijoulet et al. 2023).

Ejemplo

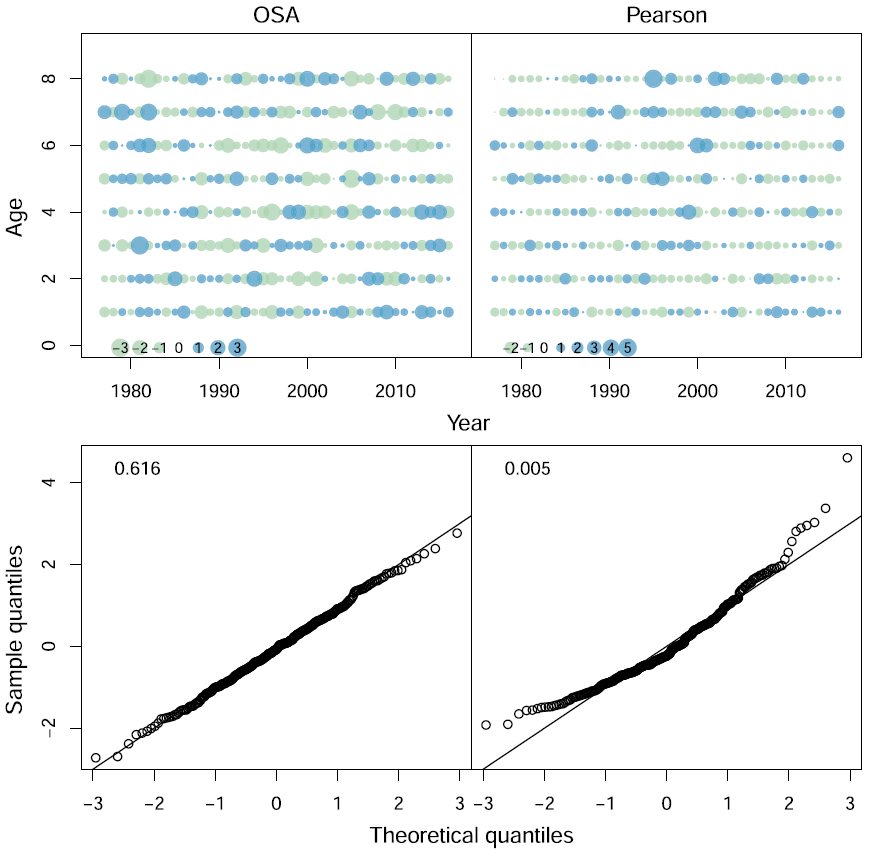
Trijoulet et al. (2023)

Definición

Los OSA residuals tiene las siguientes características:

• Independientes
• Normalmente distribuidos
• Media cero
• Varianza igual a uno

Definición

Utilizado para las siguientes distribuciones de error (datos de composición):

• Multinomial
• Dirichlet-multinomial
• Logistic-normal

WHAM: Resultados

Resultados

Hay ciertos indicadores que siempre nos interesan explorar. Primero debemos correr el modelo:

my_model = fit_wham(input = my_input, do.retro = FALSE, do.osa = FALSE)

Para explorar los estimados de efectos fijos y su error estándar:

my_model$sdrep

Resultados

Dentro del elemento $opt tambien podemos encontrar información interesante:

my_model$opt$par # parámetros (efectos fijos) optimos estimados 
my_model$opt$objective # nll value (efectos fijos)
my_model$opt$convergence # 0 = model has converged

Para explorar el gradiente final de cada parámetro (efecto fijo):

my_model$final_gradient

Resultados

Para explorar los valores esperados, y la mayoría de variables obtenidas del modelo (e.g., SSB, captura esperada, composición por edad esperada, etc), lo vemos dentro de $rep:

my_model$rep$SSB # spawning biomass vector
my_model$rep$MAA # mortalidad natural a la edad y year
my_model$rep$LAA # talla media a la edad (jan1)
my_model$rep$pred_catch_paa # composicion por edades pesqueria predicha

Se recomienda explorar todos los elementos de salida.

Resultados

Algo interesante es explorar también los elementos de $rep que tienen el character _re. Estos son las desviaciones para modelar variabilidad temporal en los diferentes componentes. Por ejemplo:

my_model$rep$WAA_re # desviaciones para peso medio nonparametric
my_model$rep$LAA_re # desviaciones para talla media nonparametric
my_model$rep$growth_re # desviaciones para talla media parametric
my_model$rep$M_re # desviaciones para mortalidad natural

WHAM: Figuras

Figuras

Existe una función principal para crear figuras y tablas a partir de un modelo en WHAM:

wham::plot_wham_output(mod = ..., # model object
                       dir.main = ..., # folder to save plots (character)
                       out.type = ...) # png or pdf 

WHAM: Proyecciones

Proyecciones

Es posible realizar proyecciones en WHAM utilizando la siguiente función:

wham::project_wham(model = ..., # model object
                   proj.opts = list(...)) # projection options 

Proyecciones

Dentro de proj.opts (lista), debemos especificar lo siguiente:

• n.yrs: (integer) número de años de proyecciones
• use.last.F: (logical) Usar terminal F para proyecciones?
• use.avg.F: (logical) Usar average F (sobre ciertos años?) para proyecciones?
• avg.yrs: (vector) Años para promediar para use.avg.F

Proyecciones

• use.FXSPR: (logical) Calcular y usar F at \(X \%\) SPR para proyecciones?
• use.FMSY: (logical) Usar F at MSY para proyecciones?
• proj.F: (vector numeric) Especificar F para proyecciones. Longitud igual a n.yrs.
• proj.catch: (vector numeric) Especificar captura agregada para proyecciones. Longitud igual a n.yrs.

Proyecciones

• cont.ecov: (logical) continuar Ecov process en proyecciones?
• proj.ecov: (matrix) especificar valores de Ecov para proyecciones.
• cont.Mre: (logical) continuar desviaciones en proyecciones?

Existen mismas opciones para crecimiento somático.

Proyecciones

• percentFXSPR: (numeric) Solo usado cuando use.FXSPR=TRUE.
• percentFMSY: (numeric) Solo usado cuando use.FMSY=TRUE.

Referencias

Aeberhard, William H., Joanna Mills Flemming, and Anders Nielsen. 2018. “Review of State-Space Models for Fisheries Science.” Annual Review of Statistics and Its Application 5 (1): 215–35. https://doi.org/10.1146/annurev-statistics-031017-100427.

Correa, Giancarlo M, Cole C Monnahan, Jane Y Sullivan, James T Thorson, and André E Punt. 2023. “Modelling Time-Varying Growth in State-Space Stock Assessments.” Edited by Pamela Woods. ICES Journal of Marine Science, August. https://doi.org/10.1093/icesjms/fsad133.

Fisch, Nicholas, Ed Camp, Kyle Shertzer, and Robert Ahrens. 2021. “Assessing Likelihoods for Fitting Composition Data Within Stock Assessments, with Emphasis on Different Degrees of Process and Observation Error.” Fisheries Research 243 (November): 106069. https://doi.org/10.1016/j.fishres.2021.106069.

Francis, R. I. C. Chris. 2014. “Replacing the Multinomial in Stock Assessment Models: A First Step.” Fisheries Research 151 (March): 70–84. https://doi.org/10.1016/j.fishres.2013.12.015.

Kristensen, Kasper, Anders Nielsen, Casper W. Berg, Hans Skaug, and Bradley M. Bell. 2016. “TMB: Automatic Differentiation and Laplace Approximation.” Journal of Statistical Software 70 (5). https://doi.org/10.18637/jss.v070.i05.

Ospina, Raydonal, and Silvia L. P. Ferrari. 2012. “A General Class of Zero-or-One Inflated Beta Regression Models.” Computational Statistics &Amp\(\mathsemicolon\) Data Analysis 56 (6): 1609–23. https://doi.org/10.1016/j.csda.2011.10.005.

Subbey, Sam. 2018. “Parameter Estimation in Stock Assessment Modelling: Caveats with Gradient-Based Algorithms.” Edited by Ernesto Jardim. ICES Journal of Marine Science 75 (5): 1553–59. https://doi.org/10.1093/icesjms/fsy044.

Thorson, James T., Kelli F. Johnson, Richard D. Methot, and Ian G. Taylor. 2017. “Model-Based Estimates of Effective Sample Size in Stock Assessment Models Using the Dirichlet-Multinomial Distribution.” Fisheries Research 192 (August): 84–93. https://doi.org/10.1016/j.fishres.2016.06.005.

Thorson, James T, Timothy J Miller, and Brian C Stock. 2022. “The Multivariate-Tweedie: A Self-Weighting Likelihood for Age and Length Composition Data Arising from Hierarchical Sampling Designs.” Edited by Ernesto Jardim. ICES Journal of Marine Science, September. https://doi.org/10.1093/icesjms/fsac159.

Trijoulet, Vanessa, Christoffer Moesgaard Albertsen, Kasper Kristensen, Christopher M. Legault, Timothy J. Miller, and Anders Nielsen. 2023. “Model Validation for Compositional Data in Stock Assessment Models: Calculating Residuals with Correct Properties.” Fisheries Research 257 (January): 106487. https://doi.org/10.1016/j.fishres.2022.106487.