Modeling time-varying growth in WHAM
Equations
Giancarlo M. Correa and Jane Sullivan
Background
The Woods Hole Assessment Model (WHAM)
- Fully state-space age-structured model
- Data: catch, indices of abundance, age compositions, empirical weight-at-age, environmental covariates
- Separability of total catch and proportions-at-age, as well as annual F and selectivity
- Random effects in selectivity, M, NAA, Q, Ecov
- Written in TMB and R (user friendly!) ( see R package ).
Stock and Miller (2021)
Somatic growth modeling
Approaches
Described in Correa et al. (2023):
Population mean size-at-age (LAA)
1. Parametric LAA
For y=1 at the start of the year (Richards 1959):
˜Ly,a={L′min+ba,a≤˜a(Lγ∞+(Lγ˜a−Lγ∞)exp(−k(a−˜a)))1/γa>˜a
Where L′min is the lower limit of the smallest length bin, ˜a is the reference age, L∞ is the asymptotic length, k is the growth rate, γ is the shape parameter. Also, b=(L˜a−L′min)/˜a.
1. Parametric LAA
For y>1:
˜Ly,a={L′min+ba,a≤˜a(˜Lγy−1,a−1+(˜Lγy−1,a−1−Lγ∞)(exp(−k)−1))1/γa>˜a
When γ=1, the equation is von Bertalanffy (Schnute 1981).
1. Parametric LAA
For any fraction θ of the year:
˜Ly,a+θ=(˜Lγy−1,a−1+(˜Lγy−1,a−1)(exp(−kθ)−1))1/γ
This is particularly important since fish also grow within a year.
1. Parametric LAA
To model time-variability, we could predict deviations on any growth parameter:
log(Pt)=μP+δP,t
Where P represents the growth parameter, and t represents years or cohorts.
The structure of these deviations δP,t could be independent or correlated over time.
2. Nonparametric LAA
Input population mean size-at-age ˜La are treated as fixed effects. We do not need any kind of parametric equation. If time-invariant growth, so ˜La,y=˜La for all y.
To model growth within a year, we use a linear interpolation between ˜La,y and ˜La+1,y+1.
2. Nonparametric LAA
If we want to model time-varying growth, we predict deviations:
˜La,y=μ˜La+δa,y
Where the structure of these deviations δa,y could be independent or correlated over time and ages, or correlated over ages, years, and cohorts (Cheng et al. 2023).
2. Nonparametric LAA
Deviations structure (correlation over years and ages):
E∼MVN(0,Σ)
E=(ε1,1,...,ε1,Y−1,ε2,1,...,ε1,Y−1,...,εA,1,...,εA,Y−1)′, Y is the number of years, and Σ is the covariance matrix:
Cov(εa,y,˜εa,y)=σGρ|a−˜a|aρ|y−˜y|y(1−ρ2a)(1−ρ2y)
where −1<ρa<1 and −1<ρy<1 are the autocorrelation coefficients (fixed effects).
2. Nonparametric LAA
We could also estimate partial autocorrelation coefficients by year, age and cohorts (Cheng et al. 2023).
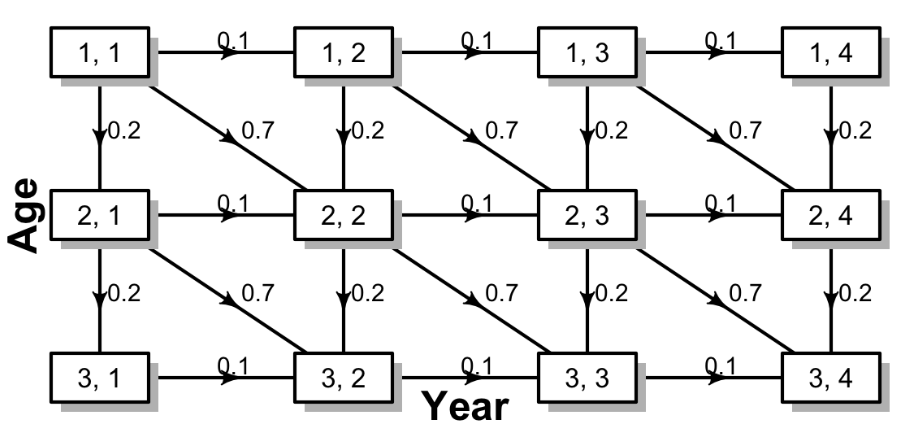
3. Semiparametric LAA
Only used to model time-varying growth. It is a combination of the previous two approaches. We follow these steps:
We calculate the population mean size-at-age at the start of the year using a parametric equation (e.g., von Bertalanffy).
Predict deviations from the values calculated in the previous step. Structure could be independent or correlated over time and ages.
Calculate population mean size-at-age within a year using linear interpolation.
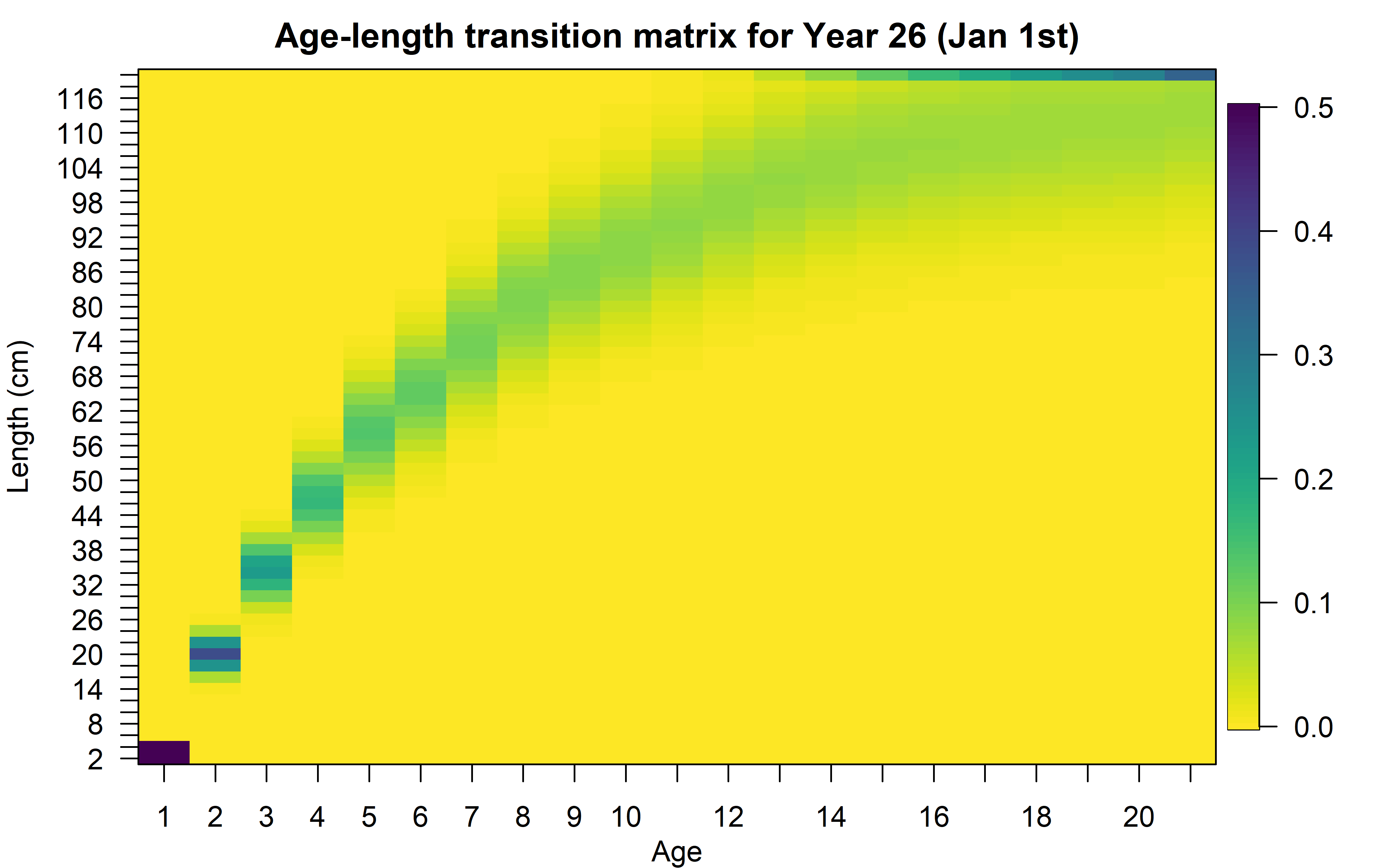
Transition matrix
Distribute the information of each age among length bins:
φy,l,a={Φ(L′min∗−Ly,aσy,a)l=1Φ(L′l+1−Ly,aσy,a)−Φ(L′l−Ly,aσy,a)1<l<nL1−Φ(L′max−Ly,aσy,a)l=nL
Φ is the cumulative standard normal distribution, L′min∗ is the smallest length bin, l is the length bin index, nL is the number of length bins, and σy,a is the standard deviation of lengths for age a.
Transition matrix
σy,a is calculated from two parameters: σ˜a y σA:
σy,a=σ˜a+(σA−σ˜aL∞−L˜a)(˜Ly,a−L˜a)
For the nonparametric LAA approach, we use LA instead of L∞ and L1 instead of L˜a.
Transition matrix
Population mean weight-at-age (WAA)
Approaches
1. Parametric WAA
When we model the population mean size-at-age, we can use the length-weight relationship:
Wl=Ω1LlΩ2
Where Ω1 and Ω2 are parameters (fixed effects).
We could also model time-varying L-W parameters (independent or correlated over time).
1. Parametric WAA
Then, to calculate the population mean weight-at-age:
Wy,a=∑lφy,l,aWl
2. Nonparametric WAA
Same approach as described for the nonparametric LAA.
We have a vector of population mean weight-at-age ˜Wa at the start of a year, treated as fixed effects. For time-invariant growth, then ˜Wa,y=˜Wa for every y.
The mean weight-at-age within a year is calculated as:
˜Wy,a+θ=˜Wy,a(Gy,a)θ
Where Gy,a=˜Wy+1,a+1/˜Wy,a.
2. Nonparametric WAA
To model temporal variability, we can predict deviations:
˜Wa,y=μ˜Wa+δa,y
Where these deviations δa,y can be independent or correlated over time and ages, or correlated over time, ages, and cohorts.
Selectivity
Size-based selectivity
Originally, only selectivity-at-age functions were available.
New functions added:
Age double normal (6 parameters).
Length logistic (2 parameters).
Length decreasing logistic (2 parameters).
Length double normal (6 parameters).
Environmental covariates
Environmental covariates
We could link a environmental covariate (Xy) to any of the growth parameters previously presented. For instance:
Gy=μGexp(βXy)
Where G is a growth parameter. For the nonparametric approaches, the environmental covariate will affect all ages equally (same β for all ages).
Observational model
Expected catch-at-age and length
We use:
ˆCy,f,l,a=φy,l,aSy,f,lSy,f,aFy,fNy,a1−exp(−Zy,a)Zy,a
Where f represents the fisheries and Zy,a is calculated using aggregated F and selectivity-at-age.
Age and length compositions
First, we sum over ages or lengths:
ˆCy,f,a=∑lˆCy,f,l,aˆCy,f,l=∑aˆCy,f,l,a
Then, we calculate the marginal composition (proportions):
ˆpy,f,a=ˆCy,f,a∑aˆCy,f,aˆpy,f,l=ˆCy,f,l∑lˆCy,f,l
Aggregated catch
We calculate:
ˆCy,f=∑aWy,aˆCy,f,a
Where Wy,a is the population mean weight-at-age that corresponds to the fishery f (year fraction).
Index of abundance
We calculate:
ˆIy,i,l,a=φy,l,aSy,i,lSy,i,aNa,yexp(−fy,iZa,y)
Where i is the index of abundance and fy,i is the year fraction when the survey takes place.
Index of abundance
We then calculate the summation over ages or lengths:
ˆIy,i,a=∑lˆIy,i,l,aˆIy,i,l=∑aˆIy,i,l,a
Then, we calculate the marginal composition (proportion):
ˆpy,i,a=ˆIy,i,a∑aˆIy,i,aˆpy,i,l=ˆIy,i,l∑lˆIy,i,l
Index of abundance
The aggregated index value (in weight):
ˆIy,i=Qy,i∑aWy,aˆIy,i,a
Where Q is the catchability and Wy,a is the population weight-at-age that corresponds to that index.
For the index value in numbers, we simply omit Wy,a.
Statistical model
Age composition
Likelihood components
- Multinomial. No parameters.
- Dirichlet-multinomial saturating (Francis 2014). 1 parameter.
- Logistic normal (Francis 2014). 1 parameter.
- Logistic normal with autocorrelation. 2 parameters.
- Logistic normal 01-inflated (Ospina and Ferrari 2012). 3 parameters.
- Multivariate-tweedie (James T. Thorson, Miller, and Stock 2022). 2 parameters.
- Linear Dirichlet multinomial (James T. Thorson et al. 2017). 1 parameter.
Length composition
Likelihood components
- Multinomial. No parameters.
- Dirichlet-multinomial saturating. 1 parameter.
- Linear Dirichlet multinomial. 1 parameter.
Thanks
Collaborators: Cole Monnahan, James Thorson, Andre Punt, Tim Miller, Steve Barbeaux, Peter Hulson
Contact:
gmoron@azti.es
Find these slides at:
giancarlomcorrea.netlify.app
References
Cheng, Matthew LH., James T. Thorson, James N. Ianelli, and Curry J. Cunningham. 2023. “Unlocking the Triad of Age, Year, and Cohort Effects for Stock Assessment: Demonstration of a Computationally Efficient and Reproducible Framework Using Weight-at-Age.” Fisheries Research 266 (October): 106755. https://doi.org/10.1016/j.fishres.2023.106755.
Correa, Giancarlo M, Cole C Monnahan, Jane Y Sullivan, James T Thorson, and André E Punt. 2023. “Modelling Time-Varying Growth in State-Space Stock Assessments.” ICES Journal of Marine Science 80 (7): 2036–49. https://doi.org/10.1093/icesjms/fsad133.
Francis, R. I. C. Chris. 2014. “Replacing the Multinomial in Stock Assessment Models: A First Step.” Fisheries Research 151 (March): 70–84. https://doi.org/10.1016/j.fishres.2013.12.015.
Ospina, Raydonal, and Silvia L. P. Ferrari. 2012. “A General Class of Zero-or-One Inflated Beta Regression Models.” Computational Statistics and Data Analysis 56 (6): 1609–23. https://doi.org/10.1016/j.csda.2011.10.005.
Richards, FJ. 1959. “A Flexible Growth Function for Empirical Use.” Journal of Experimental Botany 10 (2): 290–301. https://doi.org/10.1093/jxb/10.2.290.
Schnute, Jon. 1981. “A Versatile Growth Model with Statistically Stable Parameters.” Canadian Journal of Fisheries and Aquatic Sciences 38 (9): 1128–40. https://doi.org/10.1139/f81-153.
Stock, Brian C., and Timothy J. Miller. 2021. “The Woods Hole Assessment Model (WHAM): A General State-Space Assessment Framework That Incorporates Time- and Age-Varying Processes via Random Effects and Links to Environmental Covariates.” Fisheries Research 240 (August): 105967. https://doi.org/10.1016/j.fishres.2021.105967.
Thorson, James T., Kelli F. Johnson, Richard D. Methot, and Ian G. Taylor. 2017. “Model-Based Estimates of Effective Sample Size in Stock Assessment Models Using the Dirichlet-Multinomial Distribution.” Fisheries Research 192 (August): 84–93. https://doi.org/10.1016/j.fishres.2016.06.005.
Thorson, James T, Timothy J Miller, and Brian C Stock. 2022. “The Multivariate-Tweedie: A Self-Weighting Likelihood for Age and Length Composition Data Arising from Hierarchical Sampling Designs.” Edited by Ernesto Jardim. ICES Journal of Marine Science, September. https://doi.org/10.1093/icesjms/fsac159.
© AZTI 2023. Todos los derechos reservados.
Modeling time-varying growth in WHAM Equations Giancarlo M. Correa and Jane Sullivan