Best practices for modeling time-varying growth in state-space stock assessments
Giancarlo M. Correa1,2, Cole Monnahan3, Jane Sullivan4, James T. Thorson3, Andre E. Punt2
1AZTI, Marine Research, Sukarrieta, Spain. 2School of Aquatic and Fishery Sciences, University of Washington, Seattle, WA, USA. 3Alaska Fisheries Science Center, NOAA, Seattle, WA, USA. 4Alaska Fisheries Science Center, NOAA, Juneau, AK, USA
Somatic growth
Somatic growth
- Definition: the increase in size or weight of a fish.
- In stock assessments: at the stock level.
- Growth and recruitment are contributors to the stock biomass.
- Time-variable:
- By year, cohort, or age.
- Affected by internal and external factors.
Somatic growth in assessment models
- Not explicitly modeled in surplus production models.
- Accounted for in VPA and SCAA using empirical weight-at-age.
- Explicitly modeled in some integrated models (commonly assumed to be time-invariant).
- Ignoring temporal variability may lead to biased results.
State-space models
State-space models
Process equation: E[zt∣zt−1]=h(zt−1,θ)
Observation equation: E[yt∣zt]=g(zt,θ)
θ: vector of all unknown model parameters (fixed effects).
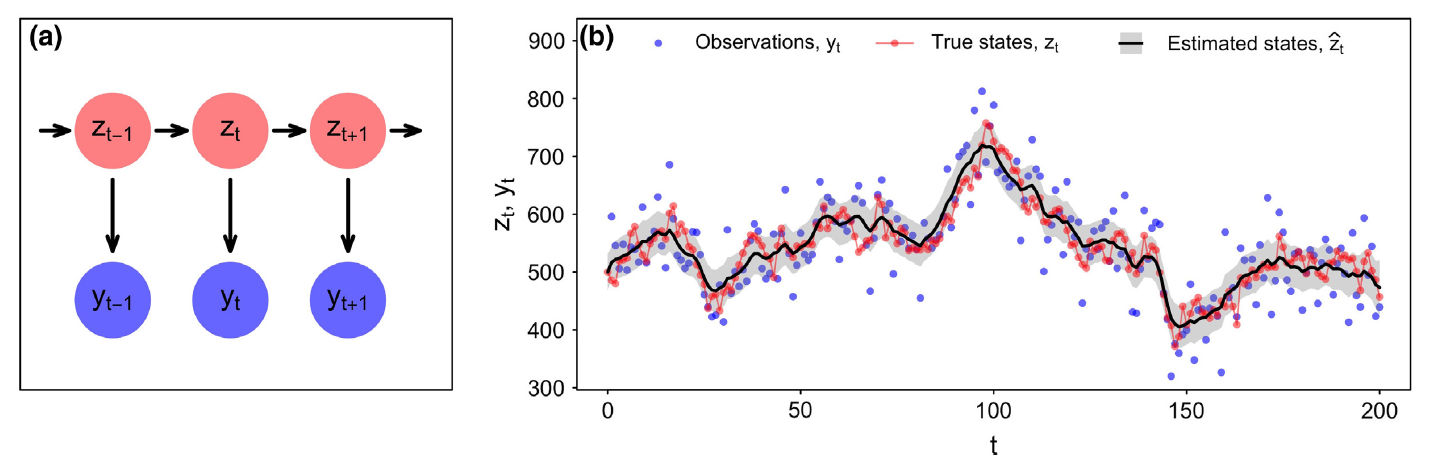
Auger-Méthé et al. (2021)
The Woods Hole Assessment Model (WHAM, Stock and Miller et al. 2021)
- Fully state-space age-structured model
- Data: catch, indices of abundance, age compositions, empirical weight-at-age, environmental covariates (Ecov)
- Separability of total catch and proportions-at-age, as well as annual F and selectivity
- Random effects in selectivity, M, NAA, Q, Ecov
- Written in TMB and R (user friendly!) ( see R package ).
Growth in state-space models
Growth in state-space models
- Goal: implement a flexible framework to model population mean length or weight at age in WHAM.
- Data:
- Length compositions
- Conditional age at length (CAAL)
- Ageing error
- Observed mean weight at age
- Parameters:
- Population mean length at age (LAA)
- Length-weight (LW) relationship
- Population mean weight at age (WAA)
Growth modeling overview
Correa et al. (2023)
LAA parametric approach
- von Bertalanffy (k, L∞, L˜a)
- Richards (k, L∞, L˜a, γ)
Length-at-age variability incorporated through two parameters (SD˜a and SDA) and a transition matrix (φy,l,a).
Predicting random effects:
log(Gt)=μG+δt
G is a growth parameter, t represents year or cohort, δ are random effects (iid or AR1 structure).
LAA nonparametric approach
Population mean length at age (La) assumed to be fixed effects. SD˜a and SDA still needed.
Time variability can be modeled by predicting random effects:
log(ˆLy,a)=μLa+δy,a
δy,a can be iid, 2dAR1, or 3dGMRF.
LAA semiparametric approach
- Use parametric approach (without random effects) to calculate Ly,a.
- Predict random effects on Ly,a:
log(ˆLy,a)=μLy,a+δy,a
δy,a can be iid, 2dAR1, or 3dGMRF.
WAA parametric
Use the LW relationship:
wl=Ω1lΩ2
Random effects on Ω1 and Ω2 can also be predicted.
Use transition matrix to calculate population mean weight at age:
ˆwy,a=∑lφy,l,awl
ˆwy,a can also be fitted to ˉwy,a (observed mean weight at age)
WAA nonparametric
Like the LAA nonparametric. Population mean length at age (wa) assumed to be fixed effects.
Time variability can be modeled by predicting random effects:
log(ˆwy,a)=μwa+δy,a
δy,a can be iid, 2dAR1, or 3dGMRF.
More new features
Selectivity
Originally, only selectivity-at-age functions were available.
New functions added:
Age double normal (6 parameters).
Length logistic (2 parameters).
Length decreasing logistic (2 parameters).
Length double normal (6 parameters).
More new features
Environmental covariates
New growth-related parameters can be linked to an environmental covariate. For example:
Pt=Pexp(β1Xt)
P is the base state (parameter) value. Other links are also available (polynomials). Lags can be modeled.
Applications
Methods applied to three stocks in Alaska:
- Gulf of Alaska Walleye pollock: age data, observed mean weight at age, WAA nonparametric.
- Gulf of Alaska Pacific cod: length and CAAL data, LAA parametric.
- Eastern Bering Sea Pacific cod: length data, LAA parametric with time-varying L˜a.
See Correa et al. (2023) Modeling time-varying growth in state-space stock assessments. ICES Journal of Marine Sciences.
Good practices
Strategies that have been shown through research and evaluation to be effective and/or efficient, and to reliably lead to a desired result.
Simulation experiment
Goal: provide guidelines for growth modeling in state-space assessment models under diverse scenarios.
- Data type: age compositions vs length compositions vs CAAL (random vs stratified sampling).
- Data source: fishery vs survey.
- Data quality: data rich vs data poor.
- Modeling approach: parametric vs nonparametric vs semiparametric vs Ecov.
- Time-varying parameter: changes in k, L∞ or L˜a.
Simulation experiment
Methodology:
Operating model: simulates the true population dynamics. Changes in growth by varying k, L∞ or L˜a.
Sample data from operating model.
Estimation model uses sampled data with assumptions on the population dynamics.
Preliminary results
Conclusions
- Expansion of the applicability of state-space assessment models.
- Implementation of a flexible framework to model time-varying growth in state-space assessment models.
- Recommendations to model time-varying growth under diverse scenarios.
Thanks
Tim Miller, Brian Stock, Jim Ianelli, Steve Barbeaux, Peter Hulson
Contact:
gmoron@azti.es
Find more information:
tinyurl.com/wham-growth
ICES Annual Sciences Conference 2023
Best practices for modeling time-varying growth in state-space stock assessments Giancarlo M. Correa 1,2 , Cole Monnahan 3 , Jane Sullivan 4 , James T. Thorson 3 , Andre E. Punt 2 1 AZTI, Marine Research, Sukarrieta, Spain. 2 School of Aquatic and Fishery Sciences, University of Washington, Seattle, WA, USA. 3 Alaska Fisheries Science Center, NOAA, Seattle, WA, USA. 4 Alaska Fisheries Science Center, NOAA, Juneau, AK, USA