Incorporating length information and growth estimation in the Woods Hole Assessment Model (WHAM)

Giancarlo M. Correa\(^1\), Cole Monnahan\(^2\), Jane Sullivan\(^3\), James T. Thorson\(^2\), Andre E. Punt\(^1\)

\(^1\)University of Washington, Seattle, WA

\(^2\)Alaska Fisheries Science Center, NOAA, Seattle, WA

\(^3\)Alaska Fisheries Science Center, NOAA, Juneau, AK

Outline

State-space assessment models
The Woods Hole Assessment Model (WHAM)
- Limitations
New features in WHAM
Examples

State-space assessment models

Allows separation of both observation and process errors.

Observation equation:

\[E[Y_t \mid X_t]= g(X_t,\theta)\]

Process equation:

\[E[X_t \mid X_{t-1}] = h(X_{t-1},\theta)\]

\(X_t\) is the unobserved state at time step \(t\) and \(Y_t\) are observations. \(\theta\) is the vector of all unknown model parameters (fixed effects). \(X_t\) treated as random effects (Aeberhard et al. 2018).

State-space assessment models

Why use them? (Aeberhard et al. 2018, Stock and Miller, 2021)

handle structural breaks, time-varying parameters
handle missing observations
can be used to do forecasting
model complex and nonlinear relationships
less retrospective bias

The Woods Hole Assessment Model (WHAM)

Fully state-space age-structured model
Developed from ASAP3 (built in ADMB)
Data: catch, indices of abundance, age compositions, empirical weight-at-age
Environmental covariates (mechanistic approach)
Written in TMB and R (user friendly!) ( see R package ).

The Woods Hole Assessment Model (WHAM)

Random effects in:

Selectivity parameters
Natural mortality
Abundance-at-age
Catchability

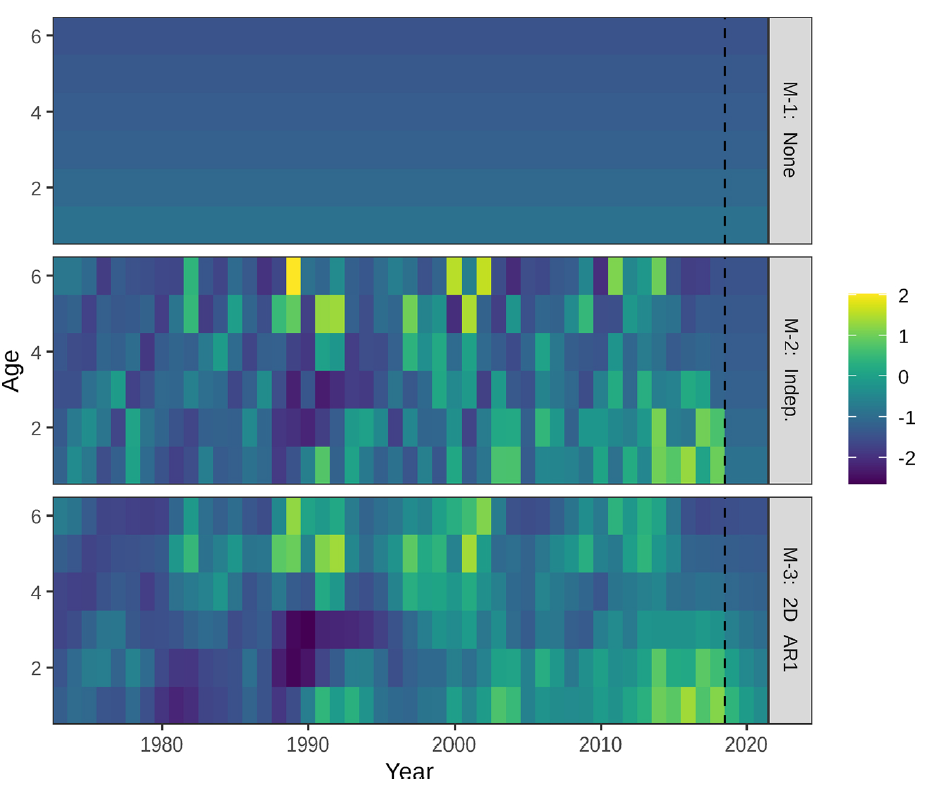Stock and Miller et al., 2021

The Woods Hole Assessment Model (WHAM)

Yellowtail flounder on the US East Coast (Stock and Miller, 2021):

The Woods Hole Assessment Model (WHAM)

Limitations:

best practices for random effects use
length information and growth modeling not available
single sex, no spatial component, no aging error
only selectivity-at-age
only input empirical weight-at-age

Great talk by Brian Stock and Tim Miller on WHAM.

WHAM expansion

Data inputs

(Marginal) length compositions
Conditional age-at-length
Input age-length transition matrix (\(\varphi_{f,l,a}\))

Growth modeling

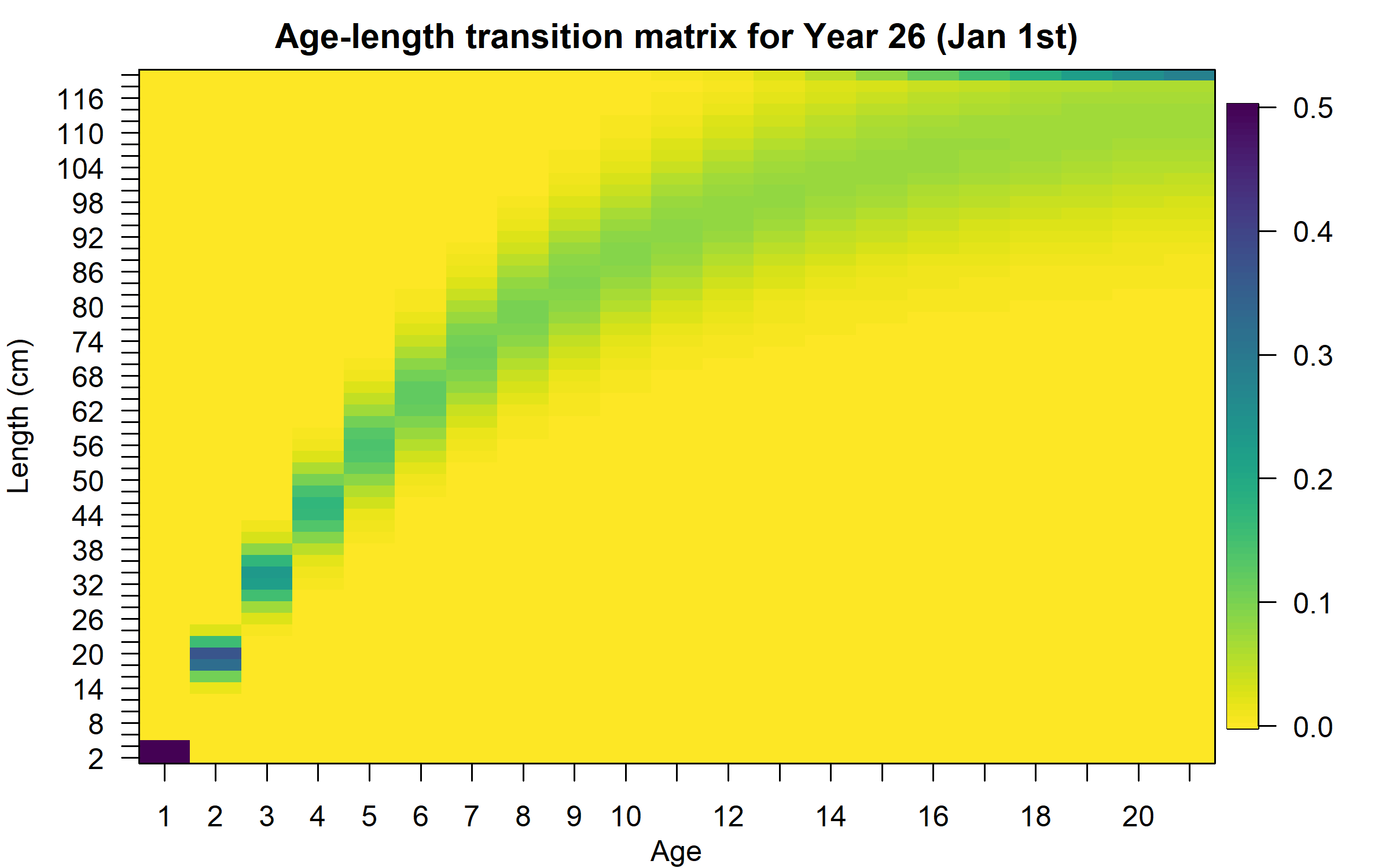
Use input age-length transition matrix

To distribute abundance-at-age to abundance-at-age and length.

Growth modeling

Use von Bertalanffy growth equation:

The mean length-at-age at the start of the year (\(y=1\)):

\[\tilde{L}_{y,a} = L_{\infty}+(L_1 - L_{\infty})exp(-k(a-1))\]

and when \(y>1\):

\[\tilde{L}_{y,a} = \begin{cases} L_1, & \mbox{if } a=1 \\ \tilde{L}_{y-1,a-1}+(\tilde{L}_{y-1,a-1}-L_{\infty})(exp(-k)-1) & \mbox{otherwise} \end{cases}\]

Growth modeling

Use von Bertalanffy growth equation:

Then, to calculate the mean length-at-age at any fraction of the year:

\[L_{y,a} = \tilde{L}_{y,a} + (\tilde{L}_{y,a} - L_{\infty})(exp(-kf_y)-1)\] \(f_y\) is the year fraction.

Growth modeling

Use von Bertalanffy growth equation:

Also, \(L_{y,a}\) and variation of length-at-age ( \(\sigma_a\) ) are used to calculate the age-length transition matrix (Stock Synthesis - SS - approach):

\[\varphi_{y,l,a} = \begin{cases} \Phi(\frac{L'_{min}-L_{y,a}}{\sigma_{y,a}}) & \mbox{for } l=1 \\ \Phi(\frac{L'_{l+1} - L_{y,a}}{\sigma_{y,a}}) - \Phi(\frac{L'_{l} - L_{y,a}}{\sigma_{y,a}}) & \mbox{for } 1<l<n_L \\ 1-\Phi(\frac{L'_{max} - L_{y,a}}{\sigma_{y,a}}) & \mbox{for } l = n_L \end{cases}\]

Growth modeling

Use von Bertalanffy growth equation:

Random effects on growth parameters can be modeled:

. . .

\[log(L_{\infty_t}) = \mu_{L_\infty} + \delta_{1,t}\]

\[log(k_t) = \mu_{k} + \delta_{2,t}\]

\[log(L_{1_t}) = \mu_{L_1} + \delta_{3,t}\]

. . .

\(t\) represents year or cohort effects and can be \(iid\) or \(AR1\).

Growth modeling

Estimate mean length-at-age:

For this case, mean length-at-age ( \(\tilde{L}_{a}\) ) are assumed to be parameters and can be estimated. \(\sigma_a\) still needed.

. . .

Time variability can be modeled by including random effects:

\[log(\tilde{L}_{y,a}) = \mu_{\tilde{L}_{a}} + \delta_{a,y}\]

\(\delta_{a,y}\) can vary by year and age.

Length-weight relationship

Optional when empirical weight-at-age not provided:

\[w_l = \Omega_1 l^{\Omega_2}\]

Random effects on \(\Omega_1\) and \(\Omega_2\) can also be estimated (like growth parameters).

. . .

Then, we can calculate the population weight-at-age at any moment during the year:

\[\hat{w}_{y,a} = \sum_l \varphi_{y,l,a}w_l\]

. . .

\(\hat{w}_{y,a}\) can also be fitted to \(w_{y,a}\) (empirical weight-at-age)

Selectivity

Originally, these selectivity-at-age functions were available:

age-specific: by age.
logistic: increasing logistic.
double-logistic
decreasing-logistic

. . .

Variability by year and parameter autocorrelation.

Selectivity

We incorporated one extra option:

double-normal: SS-like (Methot and Wetzel, 2013)

. . .

But also some selectivity-at-length functions:

len-logistic: increasing logistic at length
len-decreasing-logistic
len-double-normal

Environmental covariates

\(X_t\) (unobserved environmental variable at time \(t\) ) can be linked to any parameter presented here (Stock and Miller, 2021).

Two options for the process model:

Random walk:

\[X_{t+1}|X_{t}\sim N(X_t,\sigma_X^2)\]

\(\sigma_X^2\) is the process variance.

Environmental covariates

AR(1):

\[X_1 \sim N(\mu_X , \frac{\sigma_X^2}{1-\phi_X^2})\]

\[X_t \sim N(\mu_X (1-\phi_X) + \phi_X X_{t-1}, \sigma_X^2)\]

\(\mu_X\), \(\sigma_X^2\), and \(\mid \phi_X \mid < 1\) are the marginal mean, conditional variance, and autocorrelation parameter.

Environmental covariates

Observations \(Y_t\) are assumed to be normally distributed with mean \(X_t\) and variance \(\sigma_{Y_t}^2\):

\[Y_t \mid X_t \sim N(X_t, \sigma_{Y_t}^2)\]

\(\sigma_{Y_t}^2\) treated as known or estimated.

Environmental covariates

An environmental covariate can be linked to a state (i.e. parameter):

\[P_t = P exp(\beta_1 X_t)\]

\(P\) is the base state (parameter) value.

Other links are also available (polynomials). Lags can be modeled.

Examples

Using SS ( ss3sim, Anderson et al., 2014 ), we simulated data that was then incorporated into WHAM.

Growth variability
Conditional age-at-length (CAAL) data
Length-weight variability

Growth variability

Simulate data:

catch (one fishery)
index of abundance (one survey)
length compositions (fishery and survey)
temporal variability in asymptotic length ( \(L_\infty\) ) using PDO as the driver

Growth variability

We implemented three models in WHAM:

Random effects (by year) on \(L_\infty\)
Random effects (iid) on mean length-at-age (LAA)
Include an environmental variable (PDO), linked to \(L_\infty\)

Growth variability

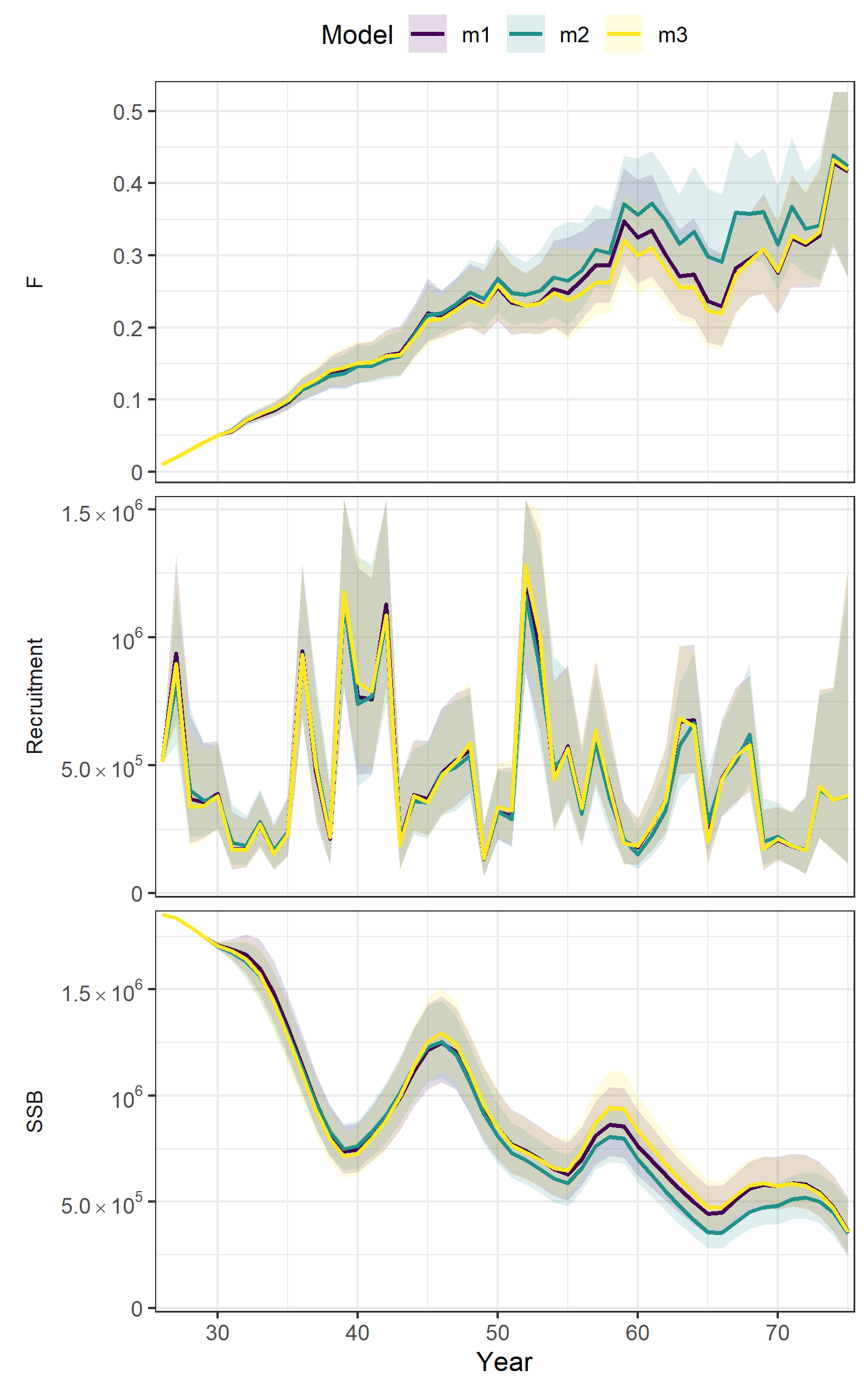
Models:

m1: random effects (by year) on \(L_\infty\)
m2: random effects on mean length-at-age (LAA)
m3: environmental variable (PDO), linked to \(L_\infty\)

Growth variability

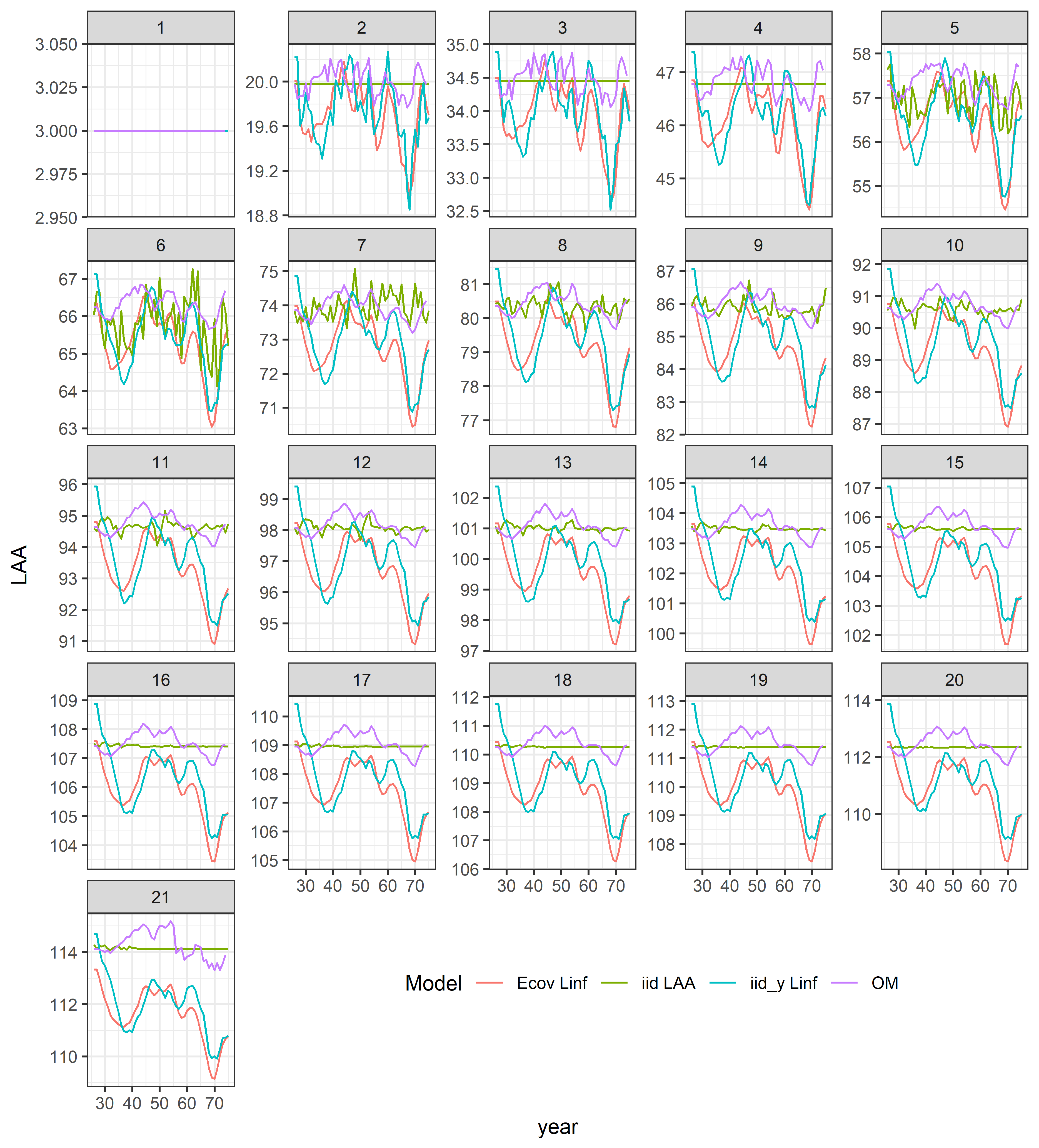
LAA: mean length-at-age at the start of the year

Still exploring these differences

CAAL data

Simulate data:

catch (one fishery)
index of abundance (one survey)
length compositions (fishery)
conditional age-at-length (survey)
selectivity-at-length

CAAL data

CAAL residuals:

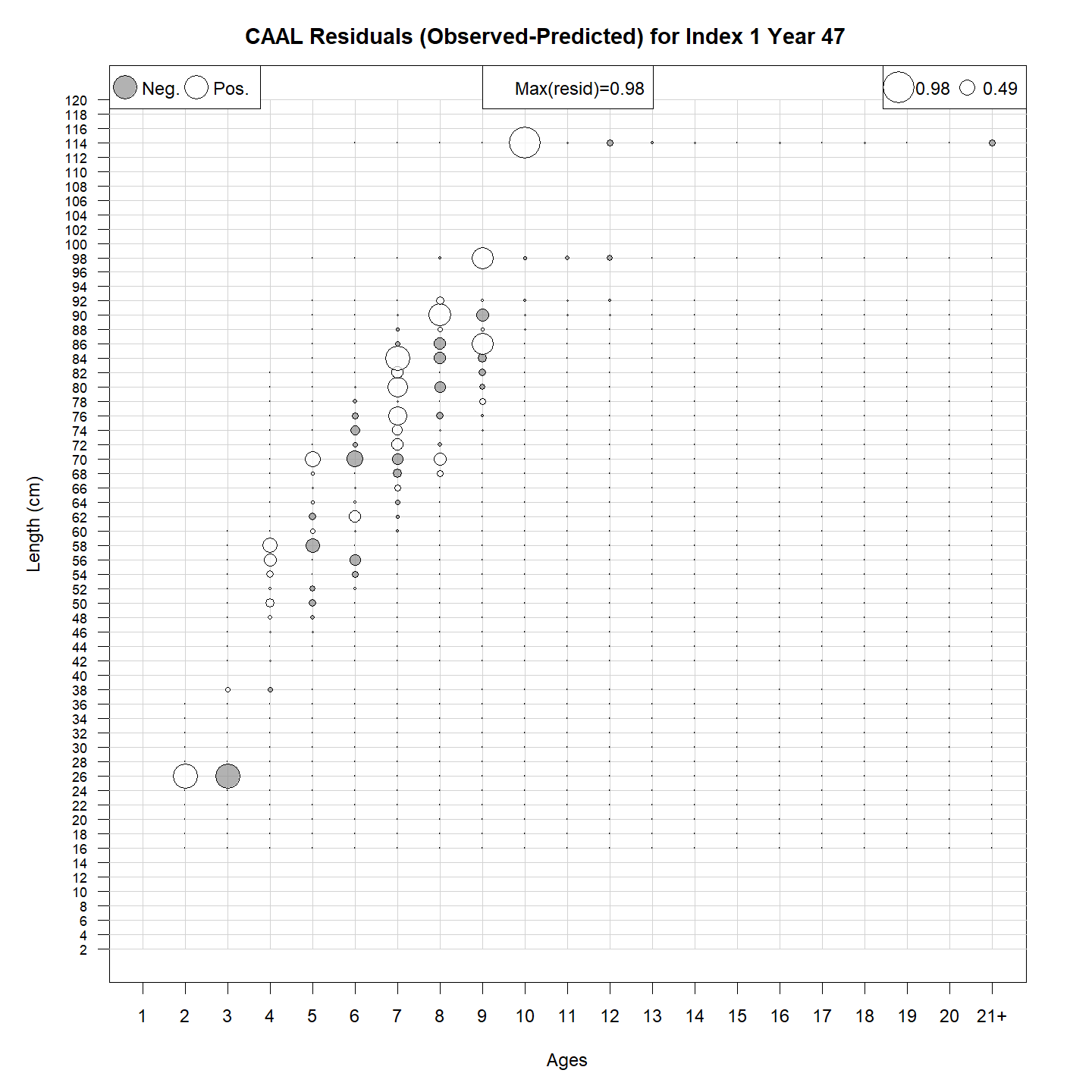
CAAL data

Estimated selectivity-at-length:

Length-weight variability

Simulate data:

catch (one fishery)
index of abundance (one survey)
length compositions (fishery and survey)
empirical weight-at-age data fitted
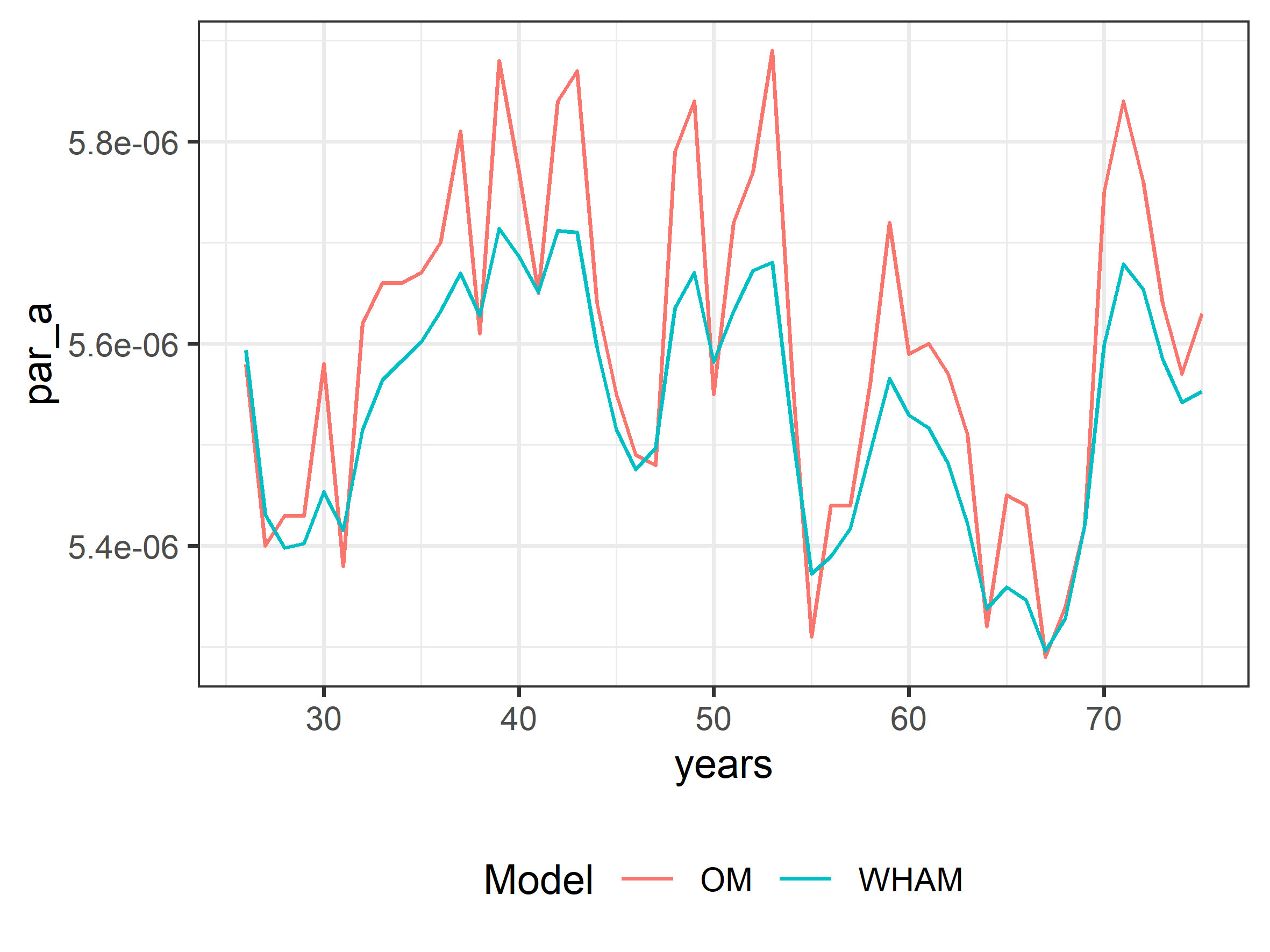
temporal variability in the \(\Omega_1\) parameter (L-W relationship)

Length-weight variability

Summary

state-space models more frequent with TMB (mostly in Europe and US East Coast)
coherent way to include climate indices into assessments (and projections!)
new tools developed in this project to apply them in the West Coast and Alaska region
future projects: sex and spatial structure
interest in organizing a workshop and applications (e.g. GOA pollock)

Thanks for listening

Contact:
gcorrea@uw.edu
giancarlo.correa@noaa.gov