Responding to climate-driven changes in growth in the modern stock assessment models
Giancarlo M. Correa1, Cole Monnahan2, Jane Sullivan3, James T. Thorson2, Andre E. Punt1
1University of Washington, Seattle, WA
2Alaska Fisheries Science Center, NOAA, Seattle, WA
3Alaska Fisheries Science Center, NOAA, Juneau, AK
Somatic growth
Somatic growth
Growth in fishes
- Stage 1: Energy to somatic growth
- Stage 2: Energy to somatic growth and sexual maturation
- Stage 3: Energy to reproduction
Morais and Bellwood (2020)
Somatic growth
Important contributor to biomass variability
Stawitz and Essington (2019)
Somatic growth
External factors that affect growth variability
Wilson et al. (2019)
State-space assessment models
State-space assessment models
Allows separation and estimation of both observation and process errors.
Observation equation: E[Yt∣Xt]=g(Xt,θ)
Process equation: E[Xt∣Xt−1]=h(Xt−1,θ)
Xt is the unobserved state at time step t and Yt are observations. θ is the vector of all unknown model parameters (fixed effects). Xt treated as random effects (Aeberhard et al. 2018).
State-space assessment models
Why use them? (Aeberhard et al. 2018, Stock and Miller, 2021)
handle structural breaks, time-varying parameters
handle missing observations
can be used to do forecasting
model complex and nonlinear relationships
less retrospective bias
The Woods Hole Assessment Model (WHAM)
- Fully state-space age-structured model
- Data: catch, indices of abundance, age compositions, empirical weight-at-age, environmental covariates
- Separability of total catch and proportions-at-age, as well as annual F and selectivity
- Random effects in selectivity, M, NAA, Q
- Written in TMB and R (user friendly!) ( see R package ).
Stock and Miller (2021)
The Woods Hole Assessment Model (WHAM)
Limitations:
- Lack of best practices for random effects use
- growth cannot be modeled internally
- selectivity-at-age options but not selectivity-at-length
- single sex, no spatial component, no aging error
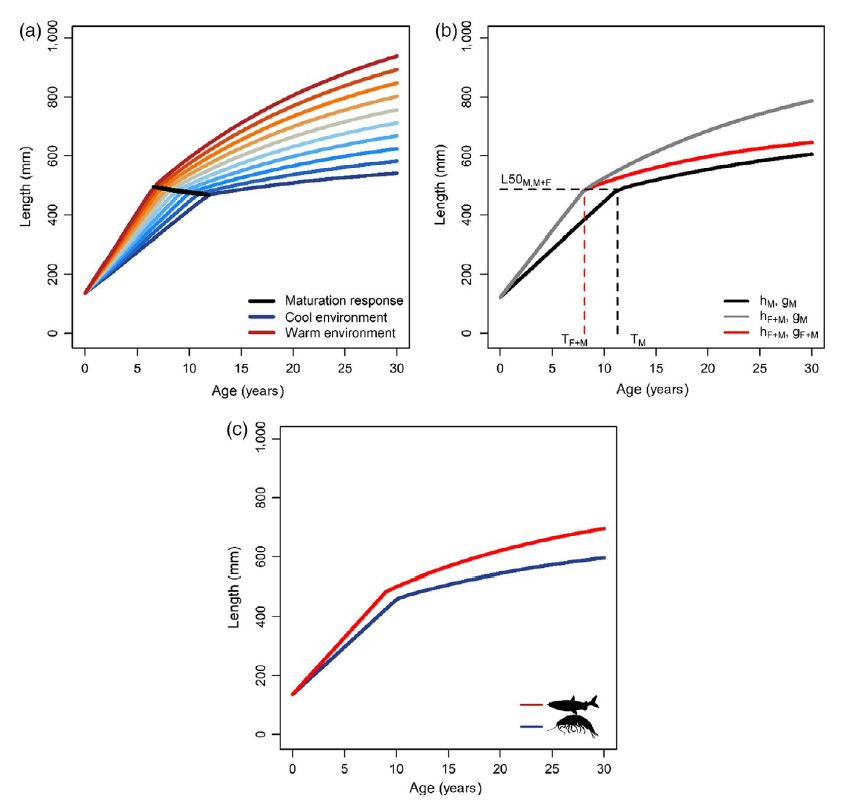
Growth modeling in state-space models
Data inputs
- (Marginal) length compositions
- Conditional age-at-length
Both are important sources of information to model growth internally.
Growth modeling
Growth modeling overview
In the population:
Mean length-at-age (LAA)
Growth equation (von Bertalanffy)
The mean length-at-age at the start of the year (y=1):
˜Ly,a=L∞+(L1−L∞)exp(−k(a−1))
a=1 is first age in WHAM. Then, when y>1:
˜Ly,a={L1,if a=1˜Ly−1,a−1+(˜Ly−1,a−1−L∞)(exp(−k)−1)otherwise
Mean length-at-age (LAA)
Growth equation (von Bertalanffy)
Then, to calculate the mean length-at-age at any fraction of the year:
Ly,a=˜Ly,a+(˜Ly,a−L∞)(exp(−kfy)−1) fy is the year fraction.
Mean length-at-age (LAA)
Growth equation (von Bertalanffy)
Random effects on growth parameters can be predicted (notice log scale):
log(L∞t)=μL∞+δ1,t
log(kt)=μk+δ2,t
log(L1t)=μL1+δ3,t
t represents year or cohort effects and can be iid or AR1.
Mean length-at-age (LAA)
LAA random effects
For this case, mean length-at-age ( μ˜La, notice log scale ) are assumed to be parameters and can be estimated. σy,a still needed.
Time variability can be modeled by predicting random effects:
log(˜Ly,a)=μ˜La+δy,a
δy,a can be iid or 2dAR1 (full variance-covariance matrix).
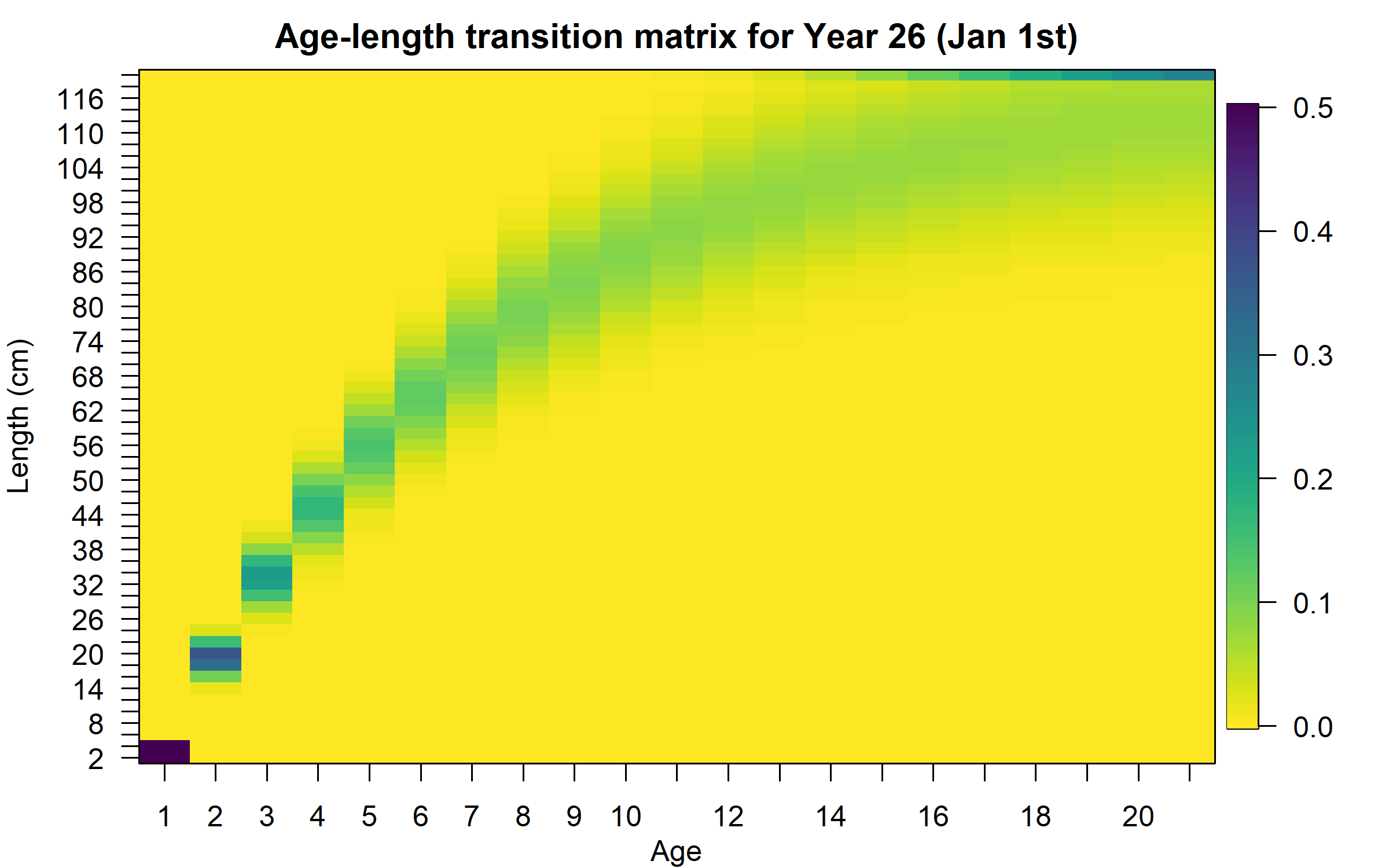
Age-length transition matrix
Also, Ly,a and variation of length-at-age ( σy,a ) are used to calculate the age-length transition matrix (Stock Synthesis - SS - approach):
φy,l,a={Φ(L′min−Ly,aσy,a)for l=1Φ(L′l+1−Ly,aσy,a)−Φ(L′l−Ly,aσy,a)for 1<l<nL1−Φ(L′max−Ly,aσy,a)for l=nL
Where Φ is standard normal cumulative density function, L′l is the lower limit of length bin l, L′min is the upper limit of the smallest length bin, L′max is the lower limit of the largest length bin, and nL is the largest length bin index.
Age-length transition matrix
Mean weight-at-age (WAA)
Length-weight relationship
Optional when empirical weight-at-age not provided:
wl=Ω1lΩ2
Random effects on Ω1 and Ω2 can also be predicted.
Then:
ˆwy,a=∑lφy,l,awl
ˆwy,a can also be fitted to wy,a (observed mean weight-at-age)
Mean weight-at-age (WAA)
WAA random effects
Like the LAA random effects. Mean weight-at-age ( μ˜Wa, notice log scale ) are assumed to be parameters and can be estimated.
Time variability can be modeled by predicting random effects:
log(˜Wy,a)=μ˜Wa+δy,a
δy,a can be iid or 2dAR1 (full variance-covariance matrix).
Selectivity
Originally, only selectivity-at-age functions were available (age-specific, logistic, double-logistic, decreasing-logistic)
New functions added:
double-normal: by age. SS-like (Methot and Wetzel, 2013)len-logistic: increasing logistic at lengthlen-decreasing-logistic: by lengthlen-double-normal: by length
Environmental covariates
WHAM separates process (random walk or AR) and observation error for environmental covariates.
An environmental covariate can be linked to a state (i.e. parameter):
Pt=Pexp(β1Xt)
P is the base state (parameter) value. Other links are also available (polynomials). Lags can be modeled.
Examples
Examples
Using SS ( ss3sim, Anderson et al., 2014 ), we simulated data that was then incorporated into WHAM.
- Growth variability
- Conditional age-at-length (CAAL) data
- Length-weight variability (condition factor)
Example 1: Growth variability
Simulated data:
- catch (one fishery)
- index of abundance (one survey)
- marginal length compositions (fishery and survey)
- temporal variability in asymptotic length ( L∞ ) using PDO as the driver
Example 1: Growth variability
We implemented three models in WHAM:
- Random effects (
iid_y) on L∞ - Random effects (
iid) on mean length-at-age (LAA) - Include an environmental variable (PDO), linked to L∞
Example 1: Growth variability
Example 2: CAAL data
Simulated data:
- catch (one fishery)
- index of abundance (one survey)
- length compositions (fishery)
- conditional age-at-length (survey)
- selectivity-at-length (double-normal)
Example 2: CAAL data
CAAL residuals:
Example 2: CAAL data
Estimated selectivity-at-length:
Example 3: Length-weight variability
Simulated data:
- catch (one fishery)
- index of abundance (one survey)
- length compositions (fishery and survey)
- empirical weight-at-age data fitted
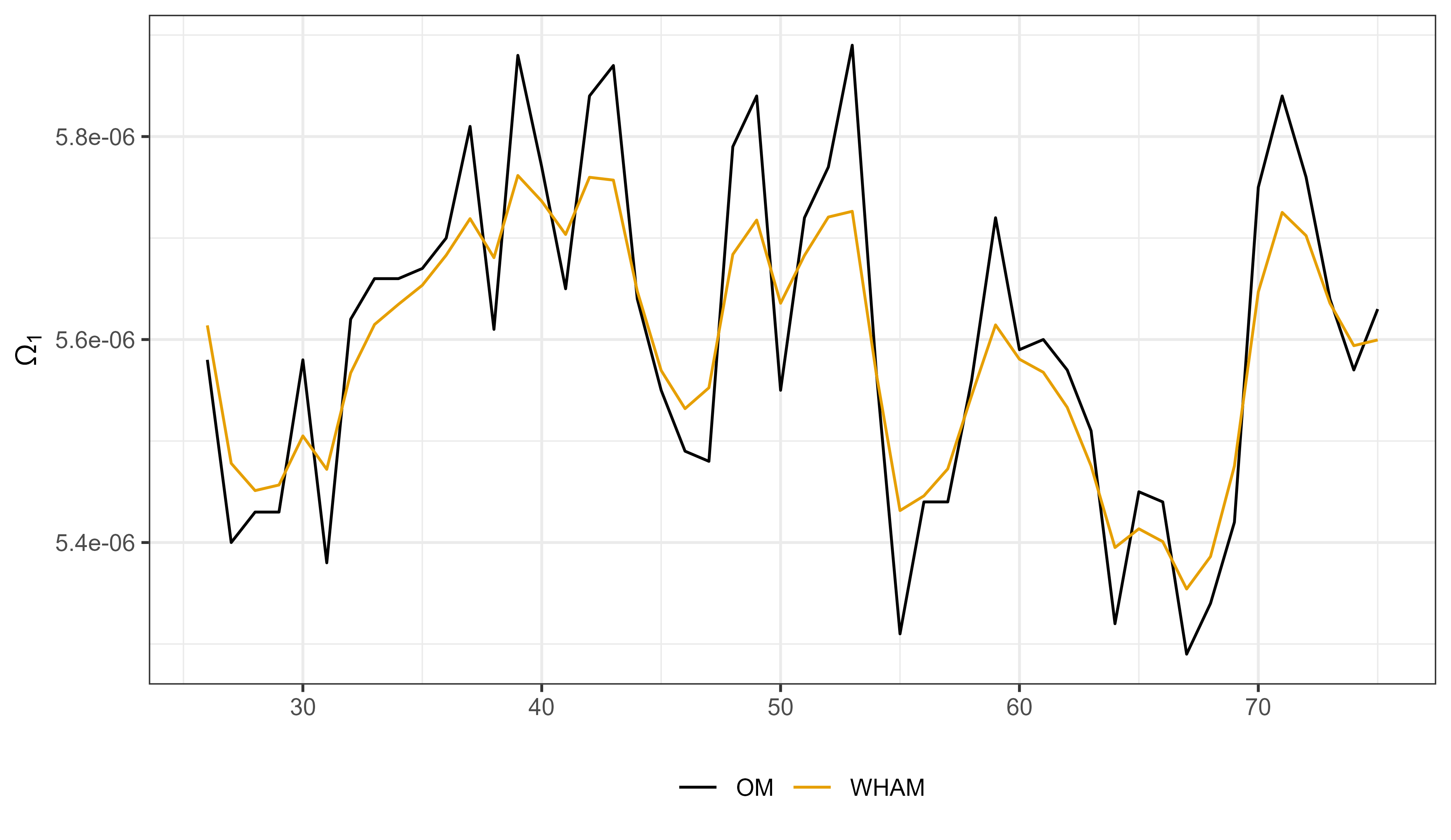
- temporal variability in the Ω1 parameter (L-W relationship)
Example 3: Length-weight variability
Walleye pollock in the Gulf of Alaska (GOA)
Model overview
Data:
- One fishery (1970 to 2021) and six surveys
- Age compositions for fishery and surveys
- Mean weight-at-age for fishery and surveys
Parameters (penalized ML for time-varying quantities):
- Time-varying fishery age selectivity
- Two Qs vary over time
- Recruitment variability
Starting model
ADMB model vs WHAM model
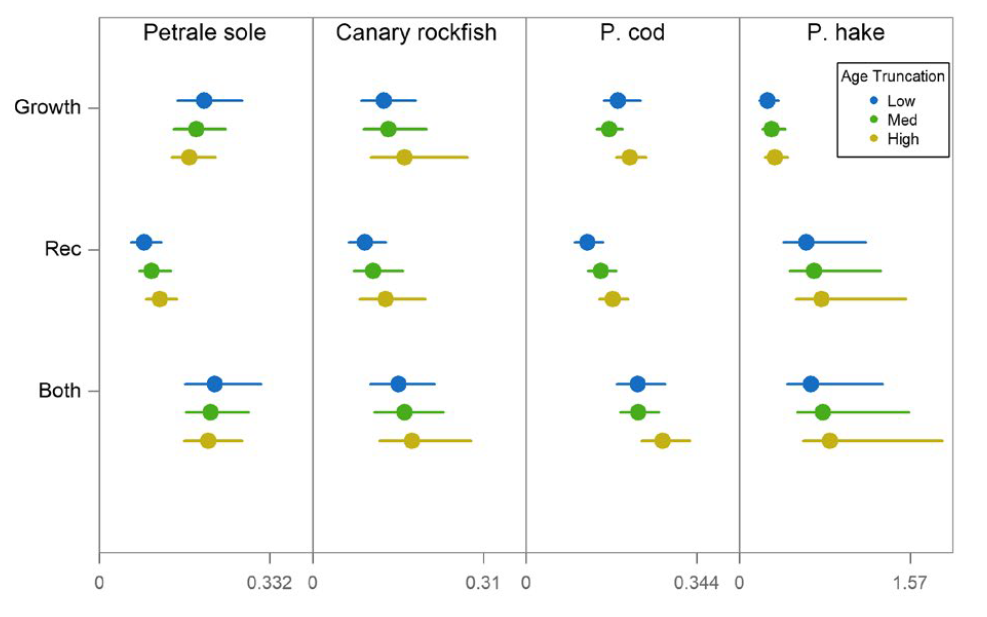
Growth variability
Observed survey fish lengths:
Growth modeling strategies
Model comparison
Mean SSB estimates:
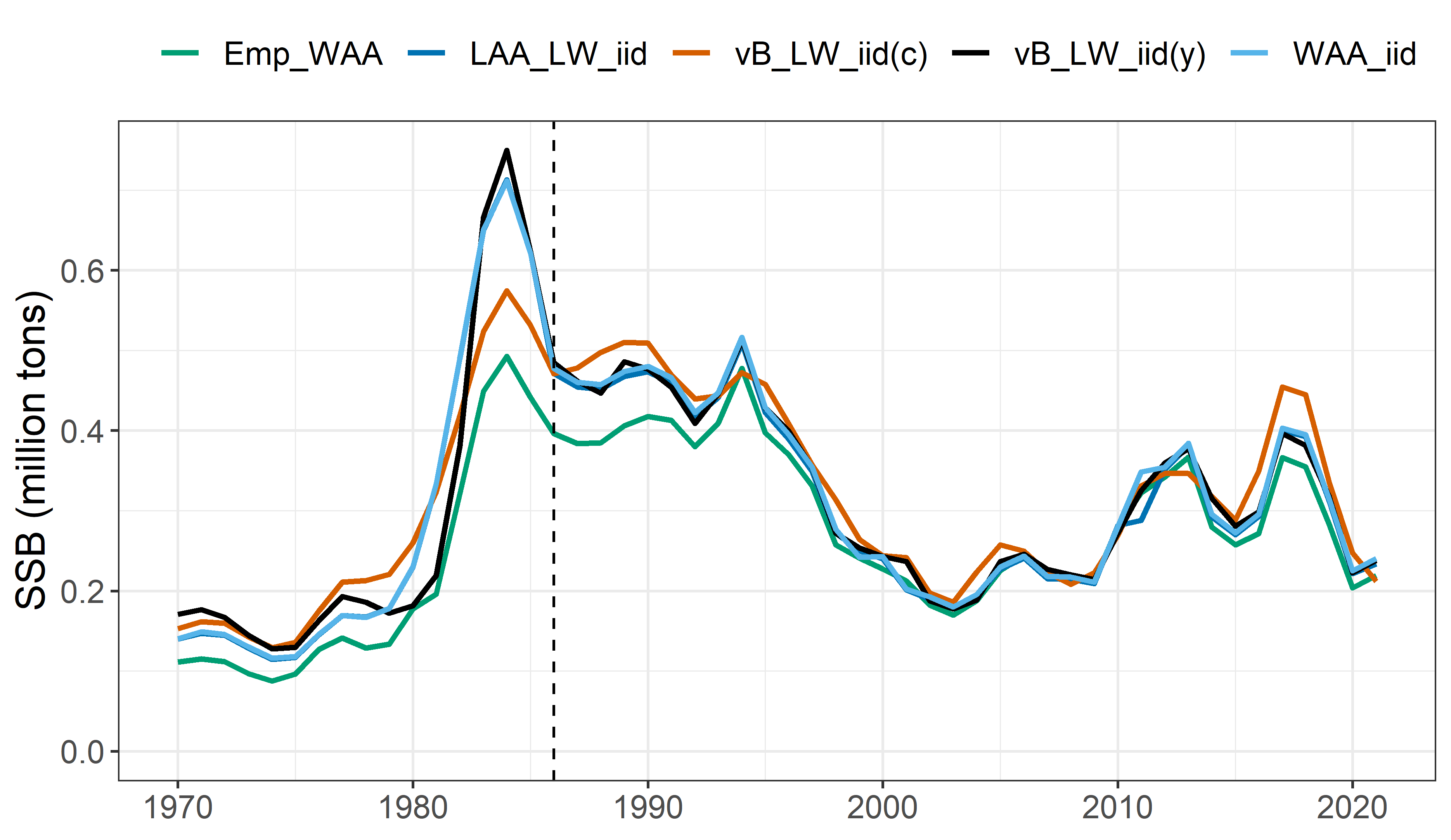
Model comparison
SSB coefficient of variation:
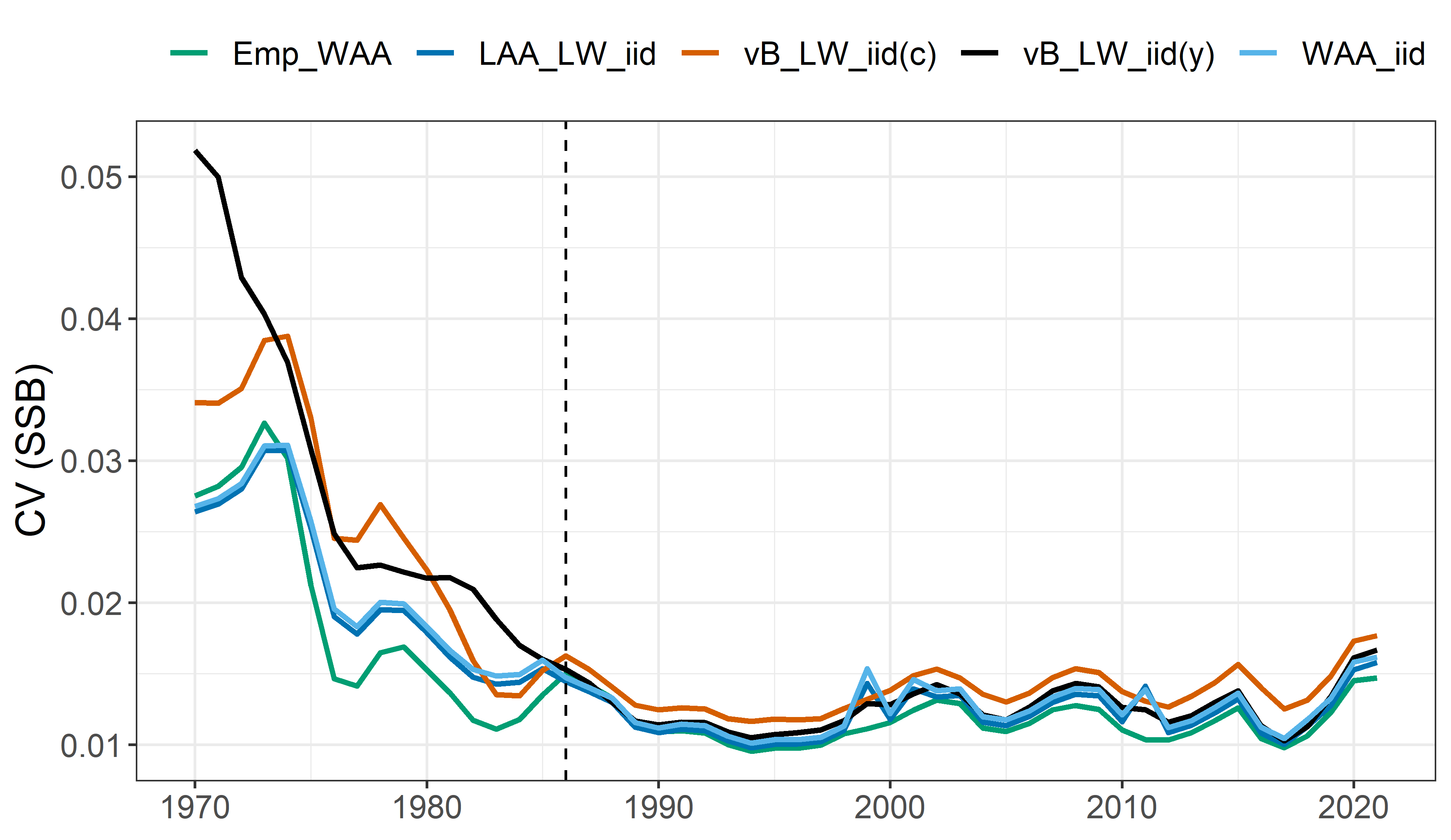
Model comparison
Growth parameters (only for growth parametric approach):
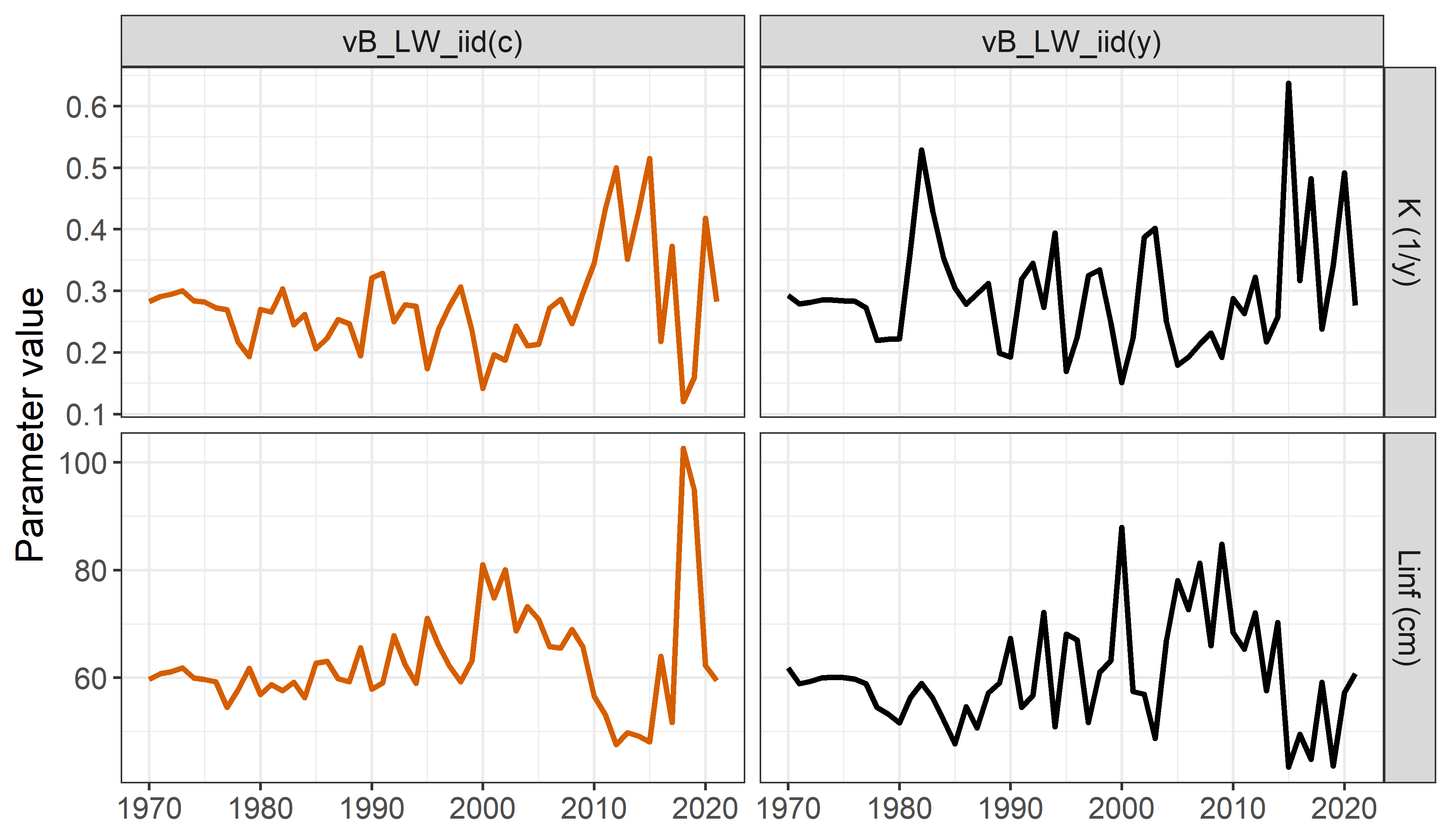
Model comparison
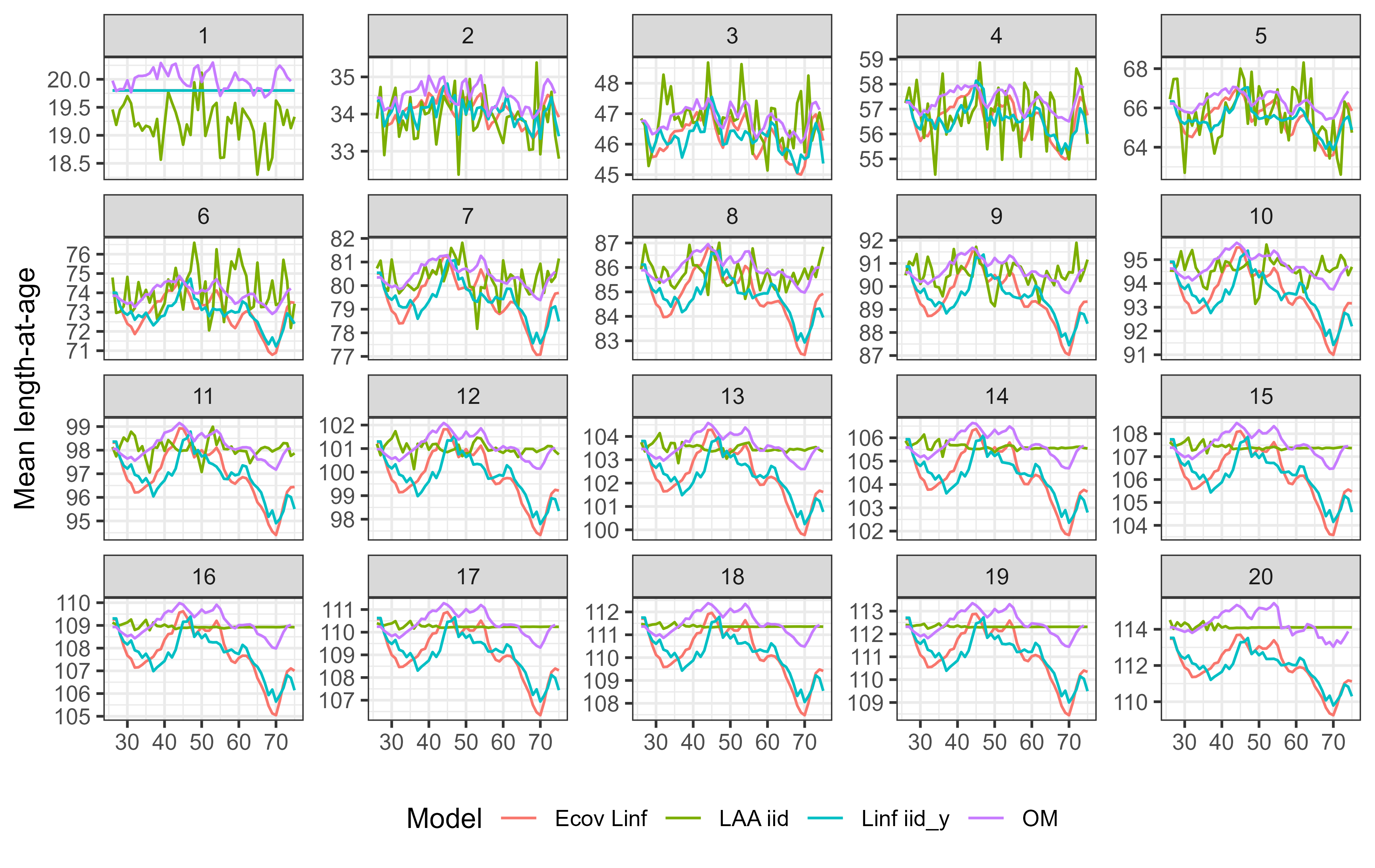
Predicted mean length-at-age (Jan 1st) vs survey observations (∼ March 1st, not included in the model):
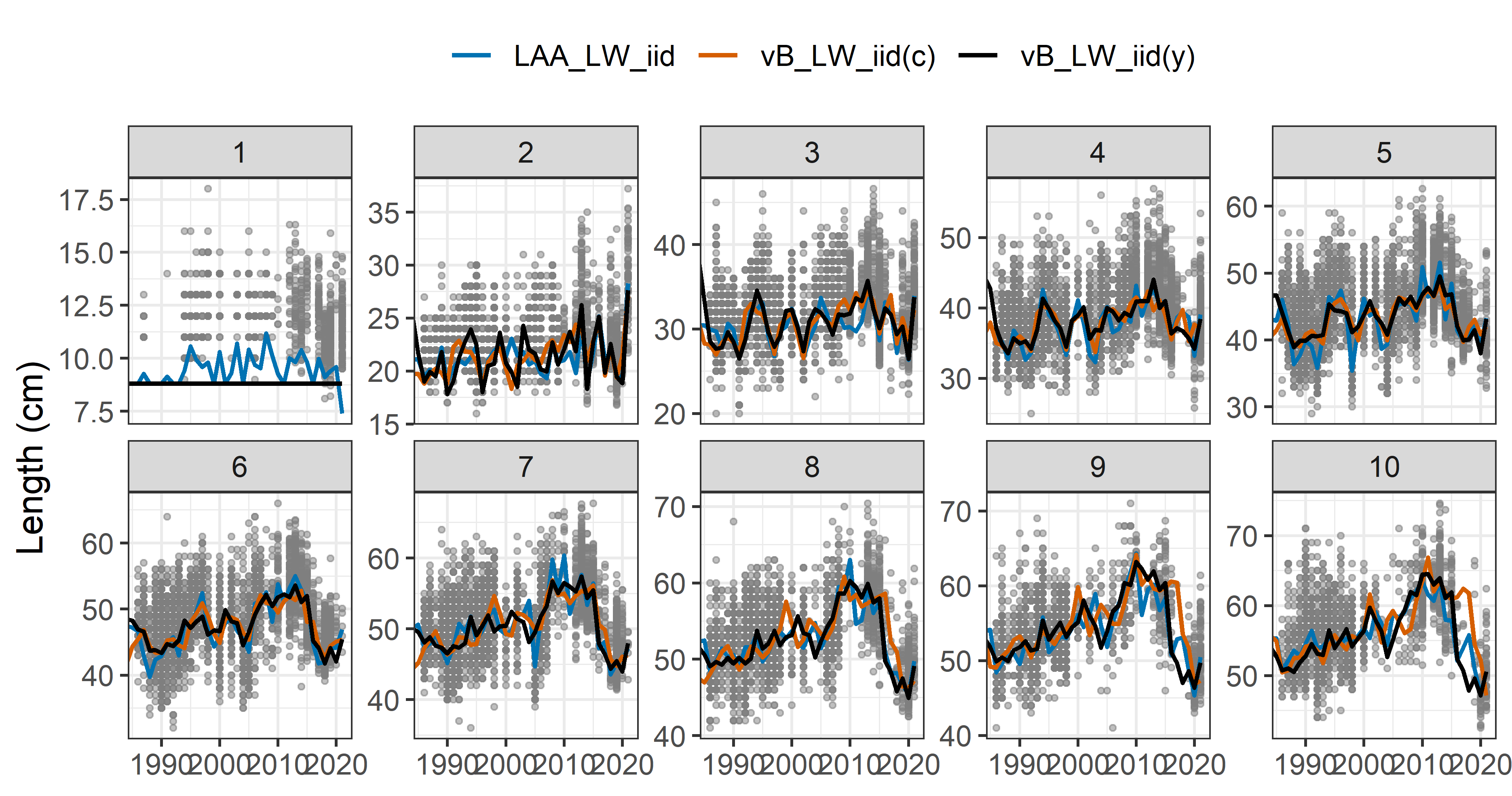
Model comparison
AIC values for models with same input data:
| Model name | (Marginal) AIC | Δ AIC |
|---|---|---|
| LAA random effects (iid) | 816.7 | 0 |
| vB equation (iidy) | 4036.6 | 3219.9 |
| vB equation (iidc) | 4761.9 | 3945.2 |
| WAA random effects (iid) | 1177.2 | 360.5 |
Final thoughts
- New tool to explore growth modeling in state-space assessment models
- Non parametric approach seems to outperform a parametric equation
- Non parametric approach is more flexible and deals with fish shrinkage
Future directions (for this project)
- Include survey length information (e.g. marginal length compositions, conditional age-at-length data)
- Add environmental covariate
- Simulation experiment: compare strategies to account for growth variability using WHAM
- Good practices for modeling growth in state-space models
Future directions (in general)
- Software development: include sex, intraannual variability, tagging data, spatial structure
- Comparison among platforms: e.g. SS vs WHAM?
- Ecological research: meaning of all random effects options
Thanks
Cole Monnahan, Jane Sullivan, Jim Thorson, Andre Punt, Tim Miller, Jim Ianelli, Brian Stock
Contact:
gcorrea@uw.edu
giancarlo.correa@noaa.gov
Find more information:
tinyurl.com/wham-growth
Responding to climate-driven changes in growth in the modern stock assessment models Giancarlo M. Correa 1 , Cole Monnahan 2 , Jane Sullivan 3 , James T. Thorson 2 , Andre E. Punt 1 1 University of Washington, Seattle, WA 2 Alaska Fisheries Science Center, NOAA, Seattle, WA 3 Alaska Fisheries Science Center, NOAA, Juneau, AK